analityczna PuRXUTM: Zbadaj, czy trójkąty ABC i KLM są przystające, jeśli: A=(−2,3), B=(5,1) i C=(3,−2) oraz K=(0,0), L=(7,−2) i M=(5,−5) No przy tym to już w ogóle nie wiem ma mieć boki tej samej długości i takie same kąty ale jak to sprawdzić ?

kylo1303: Ja bym zaczal od rysunku

PuRXUTM: a bez rysunku ?

kylo1303: Ogolnie rzecz biorac to ty masz wszystko podane, wiec obliczenie tego nie jest problemem. Kwestia tego zeby zrobic to jak najkrocej i najlatwiej.

kylo1303: Jesli nie wiesz od czego zaczac to moze od policzenia wszystkich dlugosci bokow (nie wiem czy to najkrotszy sposob, ale zawsze jakis xD)

PuRXUTM: no to powiedz jak ? Boki to wiem jak obliczyć ale jak kąty ?

kylo1303: Jesli boki beda rowne to te trojkaty beda przystajace

kylo1303: A kąty mozna liczyc ze wzorku na kąt miedzy prostymi (ale trzebaby wyznaczac rownania prostych), lub z f. trygonometrycznych

PuRXUTM: kurde pomyliłem, rzeczywiście będą bo myślałem o kątach bo jak by były tylko kąty równe to by były podobne Dzięki wielkie

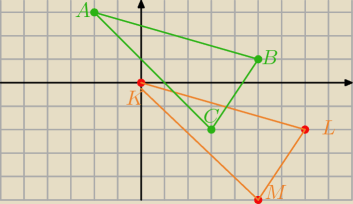
Mila: W geometrii analitycznej trzeba rysować w układzie współrzędnych. tutaj będzie Cecha bbb.(Boki równe) A=(−2,3), B=(5,1) i C=(3,−2) (0,0), L=(7,−2) i M=(5,−5) ΔABC jest obrazem ΔKLM w translacji o wektor [2,3] zatem Δ są przystające Uzasadnienie: MC^→=[2;3] LB^→=[2;3] KA^→=[2;3] II sposób; boki równe− cecha bbb ML²=2²+3² i BC²=2²+3²⇔ML=BC MK²=5²+5² i AC²=5²+5²⇔MK=AC dokończ

PuRXUTM: dzięki