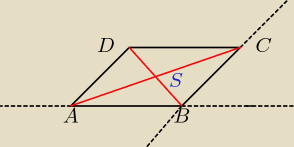
analityczna PuRXUTM: Dwa sąsiednie boki równoległoboku zawierają się w prostych o równaniach x−y−1=0 i x−2y=0. Punkt przecięcia przekątnych tego równoległoboku ma współrzędne (3,−1). Napisz równania prostych, które zawierają pozostałe boki tego równoległoboku. Zacząłem tak: Punktem wspólnym prostych AB i BC jest punkt B więc wyliczyłem go z równania i wyszło że B=(2,1)

	1
S=(3,−1). Mając te dane wyliczyłem D bo BS to chyba		BC
	2

D wyszło mi D=(4,−3) no i stanąłem Proszę o wskazówkę

Piotr: np tak : skoro masz punkt D to : prosta rownolegla do BC przechodzaca przez punkt D i podobnie z CD

PuRXUTM: o kurde ale łatwe, nie ogarnąłem

Piotr:

PuRXUTM: kurcze Piotr nie wyszło wychodzi mi że równania tych prostych mają taką postać

	1
y=−2x+5 i y=−x+1 a w odpowiedziach jest y=		x−5, y=x−7
	2

Piotr: szczerze to nie chce mi sie dokladnie liczyc ale rownolegle to a₁ = a₂ a u Ciebie jakby byly prostopadle

PuRXUTM: dobra przeliczę to kolejny raz...

Piotr: wyszlo mi :

	1
y= x−7 y=		x−5
	2

PuRXUTM: widzę błąd − jak ja nie myślę, zastosowałem właśnie dla równoległych to co dla prostopadłych...

Piotr: bylo widac na pierwszy rzut oka

PuRXUTM: no ja nie widziałem no ale rzeczywiście coś nie pasowało

Piotr: równolegle : maja ten sam wspolczynnik kierunkowy prostopadle : wspolczynnik kierunkowy jest odwrotny i o przeciwnym znaku

PuRXUTM: wiem wiem ale czemu zastosowałem tak to nie wiem

Piotr: pewnie poprzednie liczyles prostopadle glowa do gory

PuRXUTM: tak tak głowa do góry − łatwo mówić, ale dobra do roboty

Piotr: no sierżancie, do dziela !

PuRXUTM:

aniabb: ciut praktyki i będzie coraz lepiej

PuRXUTM: witaj aniabb

aniabb: witam

Piotr: witam rowniez

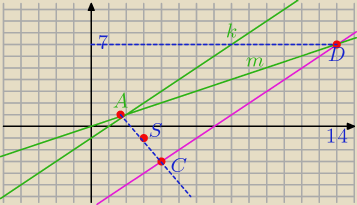
Mila: x−y−1=0 i x−2y=0⇔

	1
k: y=x−1 i x=2y⇒ m: y=		x
	2

A=(2;1) S jest środkiem AC C=(x;y) S=(3;−1)

	2+x		1+y
(3;−1)=(		;		⇔2+x=6 i 1+y=−2⇔
	2		2

C=(4;−3) prosta równoległa do k i przechodząca przez C n: y=x+b ; −3=4+b⇔b=−7 n: y=x−7 punkty przecięcia n i m ⇔x−7=1/2x⇔x=14 i y=7 S jest środkiem BD, to oblicz współrzędne punktu B

PuRXUTM: wow Mila trochę skomplikowane ale dzięki

Mila: To jest bardzo prosty sposób. Geometria analityczna jest wymagająca.