funkcja czarny: sporządź wykres funkcji y=|x−|x+2||

Wiechu: tabelka np. x −5 −4 −3 −1 0 1 3 4 5 y=... 2 2 2 0 2 2 2 2 2 wykres już chyba będziesz umiał zrobić tutaj masz współrzędne

Wiechu: sorki, że nie jest jedno pod drugim wszędzie będą już wartości 2 poza tą −1 tylko zastanawiam się czy to będzie zaokrąglany wykres w tym miejscu ale chyba nie, połącz to linią prostą

czarny: wiesz to chyba jednak nie jest takie proste, wydaje mi się, że autorowi chodzi o to aby pokazać jak został sporządzony wykres tej funkcji bez tabeli

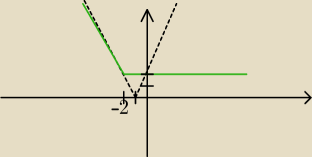
Jakub: dla x≥−2 mam x+2≥0 więc y = |x−|x+2|| = |x−(x+2)| = |x−x−2| = |−2| = 2 dla x<−2 mam x+2<0 więc y = |x−|x+2|| = |x−(−(x+2))| = |x+x+2| = |2x+2| = 2|x+1| <− to rysujesz za pomocą tabelki ale tylko dla x∊(−∞,−2) Końcowy wykres jest w przybliżeniu jak ten zielony na rysunku. Tylko go trzeba dokładniej narysować.

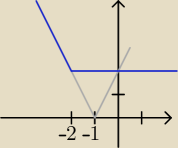
Bogdan: (−∞, −2) | <−2, +∞) −−−−−−−−−−−−−− (−2) −−−−−−−−−−−−> y = |x + x +2| | y = |x − x − 2| y = 2|x + 1| | y = 2 Dla x < −2 y = −2x − 2 Dla x ≥ −2 y = 2

czarny: Chyba właśnie o to chodziło Wielkie dzięki

Bogdan: Witam Jakubie, spóźniłem się.

agata3: hej mam takie zadanka Napisz równianie prostej przez punkty A(1,2) B(−3,−6) 2) Napisz równianie⊥i∥ do prostej x −y +2 =0 i przechodzącej przez punkt A(4,6) proszę o pomoc z góry dziękuje

Bogdan:

	−6 − 2
1. Najpierw obliczamy współczynnik kierunkowy prostej: a =		= 2.
	−3 − 1

Teraz korzystamy z wzoru: y − y₁ = a(x − x₁), gdzie x₁, y₁ to współrzędne A lub B. y − 2 = 2(x − 1) ⇒ y = 2x − 2 + 2 ⇒ y = 2x 2. Prosta k₁: y = x + 2, a₁ = 1 Prosta k₂: y = a₂x + b₂ i A(4, 6) ∊ k₂ k₂ ⊥ k₁ ⇔ a₂ * 1 = −1 ⇒ a₂ = −1 6 = −1 * 4 + b₂ ⇒ b₂ = 10 k₂: y = −x + 10 Prosta k₃: y = a₃x + b₃ i A(4, 6) ∊ k₃ k₃ || k₁ ⇔ a₂ = a₁ ⇒ a₃ = 1 6 = 1 * 4 + b₃ ⇒ b₃ = 2 k₃: y = x + 2, widzimy, że proste k₁ i k₂ pokrywają się.

agata3: dzięki za pomoc. słuchaj w przykładzie Róży Eta chyba sie pomyliła w zadaniu drugim sprawdź no chyba ma być (3,∞) sprawdź jeśli możesz . Moze to ja sie mylę. ok

agata 3: hej, mam takie zadanko. Odległość środka okręgu od cięciwy∫AB∫ wynosi 3cm Oblicz dł cięciwy jeżeli r ma 6cm Z góry dzięki

aga: długość cięciwy IABI=2*a r²=3²+a² a²=6²−3²=36−9=18 a=3√2 długość cięciwy IABI=2*3√2=6√2

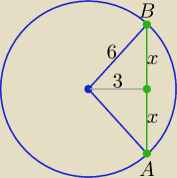
Bogdan: Zastosuj twierdzenie Pitagorasa.