aa
aa: Jeszcze jedna rzecz z liczb zespolonych:
|z+i| + | z −i | ≤ 4
Wyszło mi, że x2 + y2 ≤ 7
Więc mi wyszło koło. W przykładzie omawianym na lekcji wyszła elipsa a wolfram wogle pokazuje
coś innego.
To jak to rozumieć?
26 paź 19:45
aa: ogarnia to ktoś może?
26 paź 20:00
aa: pomoze mi ktoś? Proszę no...
26 paź 20:15
ff: jest to elipsa (z wnętrzem):
definicja elipsy − zbiór punktów których suma odległości od dwóch punktów (ognisk elipsy) jest
stała
zmienną jest z − liczba zespolona − punkt na pł. Gaussa
|z+i| + |z−i| = 4
jest to zapis:
suma odległości punktu od (0,1) i odleglości punktu od (0,−1) jest stała i wynosi 4
nierówność oznacza wnętrze elipsy
26 paź 20:48
aa: czyli to co mi wyszło : x
2 + y
2 ≤ 7 jest złe? Coś mi tu się źle policzyło tak?
26 paź 20:53
ff: to co wyliczyłeś to: |z| ≤ √7
26 paź 20:55
aa: no to ja to rozumiem jako okrąg o środku w punkcie (0,0) i promieniu √7 . a się okazuje, że
nie?
26 paź 20:57
aa: hmm?
26 paź 21:03
ff: tzn. tak: |z|<√7 i x2+y2<7 przedstawiają tą samą figurę (koło)
ale |z+i| + | z −i | ≤ 4 to nie jest |z|<√7
26 paź 21:04
aa: ale ja to robie tak:
|z+i| + | z−i| ≤ 4
| x + yi + i | + | x + yi − i| ≤ 4 => teraz liczę moduł:
√x2 + (y+1)2 + √ x2 + (y−1)2 ≤ 4 / *2
x2 + y2 +2y +1 + x2 + y2 −2y + 1 ≤ 16
2x2 + 2y2 + 2 ≤ 16 / : 2
x2 + y2 + 1 ≤ 8
x2 + y2 ≤ 7
i stąd mi tak to wychodzi. Więc wychodzi mi koło. Czyli coś robię źle, że nie wychodzi mi
elipsa.
26 paź 21:13
ff: |z+i|+|z−i|=4
|z+i|=4−|z−i|
√x2+(y−1)2=4−√x2+(y+1)2
x2+(y−1)2=16+x2+(y+1)2−8√x2+(y+1)2
y + 4 = 2√x2+(y+1)2
y2+8y+16=4x2+4y2+8y+8
4x2+3y2=8
26 paź 21:17
ff: robisz: (a + b)
2 = a
2+b
2 a tak nie jest
(
√ x2 + (y−1)2 +
√ x2 + (y+1)2)
2
= x
2 + (y−1)
2 + 2
√ x2 + (y−1)2√ x2 + (y+1)2)
2 + x
2 + (y+1)
2
to trochę komplikuje
26 paź 21:19
Mila:
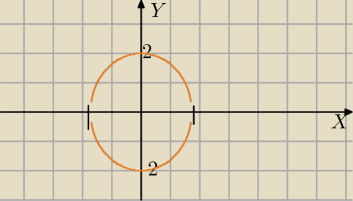
wyszło mi
4x
2+3y
2=12 /:12
| x2 | | y2 | |
| + |
| =1 elipsa − postać kanoniczna |
| (√3)2 | | 22 | |
26 paź 23:00
Mila: aa podziękuj ff, bo zrobił wielką robotę.
26 paź 23:04
aa: podziękuje chętnie ale i tak dalej do konca nie ogarniam. Bo ff ja nie robię (a+b)2 = a2 +
b2 bo znam wzory skróconego mnożenia i wiem, że będzie a2 + 2ab + b2, natomiast ten rozpis
co podałem to po uporządkowaniu, tzn. 2y i −2y daje 0 , więc to pominełem .
27 paź 00:55
aa: niewiem również skąd u Cb, wedlug Twojego rozpisu wziął się ten drugi kwadrat nad drugim
pierwiastkiem.
27 paź 00:56
aa: DOBRA JUZ KUMAM
BO JA JAK MODUŁ DO KWADRATU PODNOSZE NO TO NIE STOSUJE WZORÓW SKRÓCONEGO
MNOZENIA
ALE ZE MNIE GŁUPEK
!
27 paź 10:28