parametr Olka: Określ liczbę rozwiązań w zależności od parametru m ¦¦x−1¦−3¦=m Doszłam do x=m+3 ∨x=−m−1 ∨...(4 możliwości) i nie wiem co dalej. Widzę z wykresu ile rozw. dla jakiego m, ale jak to obliczyć? (te znaki to wart. bezwzględna

Mati_gg9225535: ja bym zrobił tak: narysowałbym wykres 1. y=|x|, który przesunąłbym o wektor 2.T_u=[1,−3] y=|x−1|−3 a następnie przekształciłbym otrzymany wykres względem tego przekształcenia 3.y=|f(x)| co daje y=||x−1|−3| po narysowaniu wykresu badasz liczę rozwiązań dla m = const

Olka: Tak zrobiłam, ale czy da sie to wyliczyc?

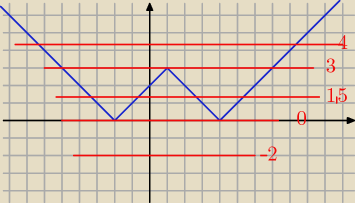
aniabb: czerwone linie to różne m=y

aniabb: jak widać dla m<0 nie przecinają się czyli rozwiązań brak

aniabb: a dla m>3 przecina się w 2 miejscach czyli 2 rozwiazania.. i rozpatrz resztę

Mati_gg9225535: dla m = 0 tez 2 rozwiazania

Olka: Dobra, rozumiem, naprawdę! Tylko pytam, czy to się da zrobić bez wykresu, obliczając?

aniabb: da się ale baaardzo czasochłonne i łatwo o błąd

Olka: Ok, dziękuję

ZKS: Dla m < 0 brak rozwiązań dla m = 0 |x − 1| − 3 = 0 ⇒ |x − 1| = 3 więc dwa rozwiązania dla m > 0 |x − 1| − 3 = m ∨ |x − 1| − 3 = −m |x − 1| = m + 3 ∨ |x − 1| = 3 − m dla 3 − m = 0 ⇒ m = 3 |x − 1| = 6 ∨ |x − 1| = 0 trzy rozwiązania dla 0 < m < 3 mamy cztery rozwiązania (m + 3 > 0 oraz 3 − m > 0) dla m > 3 dwa rozwiązania (m + 3 > 0 ale 3 − m < 0)