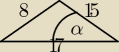
 A wiec potrzebuje kąt α. Tylko jak przekształcić twierdzenie cosinusów bo z mojego
przekształcenia wynika że cosα= c2a2+b2−2ab
A wiec potrzebuje kąt α. Tylko jak przekształcić twierdzenie cosinusów bo z mojego
przekształcenia wynika że cosα= c2a2+b2−2ab
| 152+172−82 | ||
cosα= | =......... | |
| 2*15*17 |
| −c2+a2+b2 | ||
cosα= | ||
| 2ab |
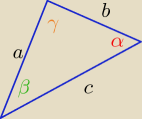
| b2+c2−a2 | ||
cosα= | ||
| 2bc |
| a2+c2−b2 | ||
cosβ= | ||
| 2ac |
| a2+b2−c2 | ||
cosγ= | ||
| 2ab |
| abc | ||
Pole trójkąta P = | , | |
| 4R |
| a*b*c | ||
R = | ||
| 4P |
| 8+15+17 | ||
p = | = 20, p−8=12, p−15=5, p−17=3, P = √20*12*5*3 = 60 | |
| 2 |
| 8*15*17 | ||
R = | ||
| 4*60 |