prosze o rozw michu: Okresl liczbe punktow wspolnych wykresu funkcji f(x)=a^x dla a>0 oraz prostej opisanej rownaniem a)y=3 b)y=−2 c)x=−1 d)x=4

Ajtek: Z wyjątkiem b masz 1 punkt wspólny. W b brak punktów wspólnych.

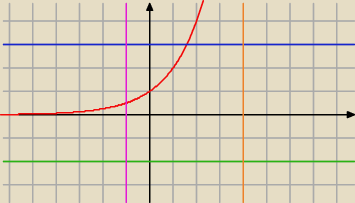
Ajtek: NIebieska y=3 Zielona y=2 Fioletowa x=−1 Pomarańczowa x=4 tutaj tego nie widać, ale ma punkt wspólny o współrzędnych [a;a⁴]

Ajtek: Zielona y=−2 oczywiście :0.

ICSP: a dla y = 1

Ajtek: Tam nie ma prostej y=1 . Ale też 1 punkt wspólny.

ICSP: mam Cie : zła odpowiedź

michu: dzieki bardzo

Ajtek: Jak zła dla a=1 masz nieskończenie wiele punktów wspólnych, a Ty pytałeś o y=1 . Zresztą f. wykładnicza jest określona dla a>0 i a≠1 .

Ajtek: Źle napisałem dla a=1 miałbyś nieskończenie...., a że a≠1 z definicji to wiemy co.

ICSP: A widzisz gdzieś tutaj założenie ze a ≠ 1 Trzeba uwzględnić wszystkie przypadki . e) y = 1 : dla a = 1 nieskończenie wiele rozwiazań dla a ≠ 1 oraz > 0 jedno rozwiązanie Dlatego obstawiam ze podpunkty a oraz b są źle zrobione

Ajtek: NIe wczytałęm się dkoładnie w treść zadania, zobaczyłem wykładniczą to pojechałem standardem . A co nie pasi w a

ICSP: dla a = 1 brak rozwiązań dla a > 0 i a ≠ 1 jedno rozwiązanie. Przynajmniej tak mi się wydaje. Lepiej zeby ktoś potwierdził te moje przypuszczenia.

Ajtek: No tak, poszedłem na łatwiznę, masz rację Ostateczne rozwiązanie: dla a=1 a − brak rozwiązań b − nieskończenie wiele c i d − 1 rozwiązanie dla a≠1 a,c,d − 1 rozwiązanie b − brak rozwiązań

ICSP: 1 = −2

Ajtek: Co znowu?

ICSP: a = 1 b − brak rozwiązań

Ajtek: Fakt .

Ajtek: To przez Twój podpunkt e wszystko .

ICSP: