rownanie okregu
maciek:
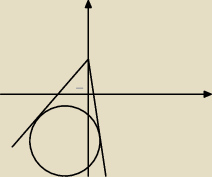
oblicz pole figury ograniczonej osia ox i prostymi stycznymi do okregu os s(−4,−5) promieniu
3sqr5 prrzechodzacymi przez A(0,2).
olga: ustalamy wzór naszych stycznych : y = ax + b , wiemy , że be jest równe 2 , w takim razie nasze
styczne będą miały wzór y = ax + 2 , jest to wzór kierunkowy, zamieńmy to na wzór ogólny : −ax
+ y − 2 = 0 , musimy teraz wyliczyć niewiadomą a : możemy to wyliczyć ze wzoru na odległość
punktu od prostej d=I Ax
0 + By
0 + C I /
√ A2 + B2 , nasze d to promień okręgu a : x
0 i
y
0 to punkty środka okręgu , podstawmy :
3
√5 = I 4a − 5 − 2 I /
√a2 + 1
3
√5√a2 + 1 = I 4a − 7 I I
2
45a
2 + 45 = 16a
2 − 56a + 49
29a
2 + 56a − 4 = 0
Δ=3600,
√Δ=60
a
1=−2 , a
2=2/29
mamy nasze wzory stycznych : y=−2x + 2 i y=2/29x +2
figurą której pole musimy obliczyć jest trójkąt, mozemy zauwazyc ze jego wysokość jest róna 2 (
z obrazka ) i musimy oblicz podstawe na która spada wysokosc, czyli podstawa jest odcinek
nalezocy do osi OX , musimy znalezc punkty przeciecia sie naszych stycznych z ta isoa by
wiedziec ile ma ona jednostek, musimy wiec wyliczyc miejsca zerowe naszych stycznych
dla stycznej y=−2x + 2 , podstawiamy y=0 :
0=−2x + 2
x=1 , czyli mamy punkt (1,0)
i dla y=2/29x + 2 równiez podstawiamy y=0 :
0=2/29x + 2 I*29
0=2x + 58
x=−29 , nasz punkt (−29,0)
czyli nasza podstawa razem ma 30
liczymy pole ze wzoru P=1/2a*h , podstawmy :
P=1/2*30*2
P=30
powodzenia

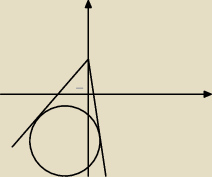 oblicz pole figury ograniczonej osia ox i prostymi stycznymi do okregu os s(−4,−5) promieniu
3sqr5 prrzechodzacymi przez A(0,2).
oblicz pole figury ograniczonej osia ox i prostymi stycznymi do okregu os s(−4,−5) promieniu
3sqr5 prrzechodzacymi przez A(0,2).
