zadanie funkcja adaś: Proszę o pomoc w rozwiązaniu : Narysuj wykres funkcji : f(x)=| |x|−1| Ja robię tak i nie wiem co jest źle.

	⎧	x dla x≥0
|x|=	⎩	−x dla <0

	⎧	x−1 dla x−1 ≥0 x≥1
|x−1|=	⎩	−x+1 dla x−1<0 x<1

	⎧	−x−1 dla −x−1≥0 x≤−1
|−x−1| =	⎩	−(−x−1) =x+1 dla −x −1<0 x>0

dobrze robię , co dalej w takim razie?

zombi: narysuj w krokach 1^o f(x)=x 2^o f(x)=|x| 3^o f(x)=|x|−1 4^o f(x)=||x|−1|

adaś: dzięki, chyba już zrobiłem , najpierw zrobiłem f(x)= |x|−1 a potem odwróciłem wykres względem Osi OY, można tak zrobić prawda?

Krzysiek : Nie nie mozna . Jesli narysowales wykres funkcji f(x)=IxI−1 − swoja droga napisz dokladnie jak go narysowales lub narysuj i teraz jesli masz dobrze narysowany wykres f(x)=IxI−1i masz otrzymac wykres f(x)=IIxI−1I to musisz to co jest pod osia OX wykresu f(x)IxI−1(tylko ta czesc wykresu ) odbixc do gory zeby to sie znalazlo nad osia OX bo masz z tego miec wartosc bezwzgledna czyli tak f(x)=IIxI−1I a wartosc bezwzgledna nie moze byc ujemna czyli nic z wykresu f(x) =IIxI−1I nie moze znajdowac sie pod osia OX Teraz jak przeksztalcisz caly wykres f(x)=IxI−1 czy to wzgledem oxi OX czy to wzgledem osi OY to nadal czesc wykresu bedzie pod osia OX . Teraz rozumiesz .

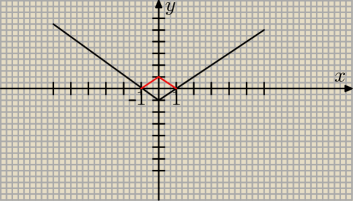
adaś: tak będzie wyglądał wykres : f(x)= |x|−1 , teraz obrócenie względem osi OY czyli to co jest pod osią x przerzucam na drugą stronę ,ten czerwone kreski a resztę wykresu zostawiam, prawda?

zombi: f(x)=|x|−1 to co co narysowales a ||x|−1| to to f(x) tylko jeszcze odbijasz to co bylo pod osia O_x na gore czyli to czerwone