trapez i jego pole ^^ pn: Witam. Mam takie zadanko i nie wiem jak zacząć Środek okręgu wpisanego w trapez prostokątny, znajduje się w odległości 4 i 8 od końców dłuższego ramienia trapezu. Oblicz pole tego trapezu. Proszę o pomoc

pn: pomoże ktoś?

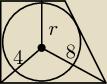Jasiu: hmm i co dalej...

pn: Jasiu. Chyba ten promień z czwórką to do góry. żeby powstał kąt prosty i z pitagorasa.... tylko tyle wiem i później zonk

Jasiu: czyli jak? weź narysuj..

bigduck: od końców ramienia a nie podstawy

bigduck: dłuższego ramienia

Jasiu: aa juz wiem... źle zrozumiałem

pn: kurcze. jak tu sie rysuje, bo nie umiem xD

Jasiu: no wlasnie sie zastanawiam...

bigduck: pomagam

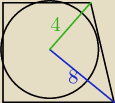pn: coś takiego.. wybaczcie za niesforny rysunek

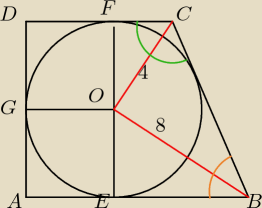bigduck: zielony − α pomarańczowy − β najpierw przydało by się udowodnić że trójkąt OBC jest prostokątny: Trapez jest czworokątem więc suma kątów wynosi 360, jak się odejmie 2 kąty proste zostanie 180 α+β=180 ∡OCB = 1/2α ∡OBC = 1/2β ∡COB = 180 − 1/2α−1/2β = 180−90 = 90 Kolejno trójkąty BCO, FCO są podobne ponieważ: ∡OCB = ∡OCF = 1/2α* ∡BOC = ∡OFC = 90 Dalej trókąty BCO, EBO są podobne ponieważ: ∡OBC = ∡OCE = 1/2α*∡BOC = ∡OEB = 90

bigduck:

	EO		OC
Następnie z tesla		=
	OB		BC

	FO		OB
i tak samo ten na górze trójkąt:		=
	OC		BC

będziesz miał wystarczająco danych do obliczenia Twojego zadania

pn: o dziękuję Ci i jestem "ona" ^^ hehe

bigduck: oj oj, przepraszam nie zauważyłem w razie problemów gg:12369915, skoro "Ona"

pn: mm ^^ dobrze. dziękuje