Okrąg wpisany w czworokąt freaky: W romb wpisano okrąg. Punkt styczności okręgu z bokiem dzieli bok na odcinki długości 4 cm i 9 cm. Oblicz długość przekątnych i wysokość rąbu. Bardzo proszę o rozwiązanie i WYJAŚNIENIE co z czego wynika.

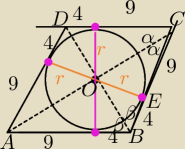
Mila: Punkty styczności są jednakowo odległe od wierzchołków kątów a=4+9=13 i h=2r W ΔCOB: promień jest prostopadły do boku w punkcie styczności( jest wysokością) ΔCOB jest prostokątny (spróbuj uzasadnić − z sumy kątów w trójkącie i wiedząc, że ∡B+∡C=180⁰) r=√4*9=6 i h=12 w ΔCOE: OC²=6²+9²⇔|OC|=√117=3√13⇔|AC|=6√13 w Δ BOE: OB²=4²+6²⇔OB|=2√13⇔|DB|=4√13