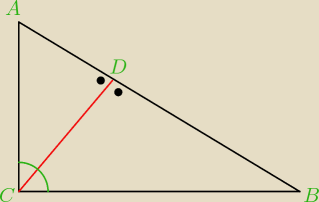
Figury podobne Daria: W trójkącie prostokatnym ABC,w którym kąt przy wierzchołku C jest prosty,poprowadzono wysokość CD.Udowodnij ze trójkąt ADC jest podobny do trójkata DBC oraz |CD|=p[|AD|*|DB|}

Daria: Momocyyy

tim: Umiem wyjaśnić druga część.

Daria: Ooo to mozesz mi pomoc

tim: {AD² + CD² = AC² {CD² + BD² = BC² {AC² + BC² = (AD + BD)² Sumuję dwa pierwsze: 2CD² + AD² + BD² = AC² + BC² Podstawiam do trzeciego: 2CD² + AD² + BD² = AD² + 2 * BD * AD + BD² Skracam i zostaje CD² = AD * BD CD = √AD * BD

tim: (cecha BBK) dwa boki i kąt położony naprzeciw dłuższego z nich A pierwsza część zapewne to, ale próbuję dopiero mam 15 lat

Daria: Dzięki

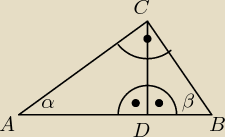
♊: mamy trójkąt ABC ∢CAB = α ∢ABC = β α+β+90^o=180^o Poprowadziliśmy wysokość |CD| i stąd mamy, że ∢CDA = ∢ BDC = 90^o Teraz miara wszystkich kątów w trójkącie ADC = 180^o = ∢DCA + α+90^o Przyrównujemy do siebie te równania zaznaczone na zielono i wychodi, ze ∢DCA = β Nie musimy robić tak samo robimy z ∢DCB i α bo nie jest to potrzebne. Opdowiedź: Trójkąty są do siebie podowbe na mocy zasady kąt−kąt.