planimetria Kulka: 1) Dany jest trapez o podstawach 2 i 8 i wysokości 4. Przekątne trapezu podzieliły go na 4 trójkąty. Oblicz ich pole. 2) Przekątne trapezu ABCD o podstawach 6 i 4 przecinają się w punkcie E. Odległość punktu E od dłuższej podstawy wynosi 3. Oblicz pole trojkąta BEC i DEC. 3) W równoległoboku ABCD punkt E jest środkiem boku AB. Pole równoległoboku wynosi 6 √3. Długość odcinka AB=6 i AD = 2. Oblicz długość odcinka EC

Mati_gg9225535: wykonalas chociaz rysukni ?

Kulka: Tak, ale nie mam pojęcia co dalej zrobić, planimetria nigdy nie była dla mnie

Mati_gg9225535: to proponuje Ci umiescic wszystkie dane na rysunku, wypisać jakie wartości są szukane a następnie przyjrzeć się wzorom, zastanow sie czego Ci brakuje do "szczęscia" i spróbuj jakoś zacząć

Kulka: Nie pisałabym tych zadań tutaj , gdybym tego wcześniej nie zrobiła. Jeżeli nie masz zamiaru pomóc tylko pouczać to wogle nie pisz.

Mila:

	2+8
Ptrapezu=		*4=20
	2

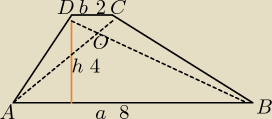
P_ΔDOA=P_ΔCOB

	2		1
ΔDOC jest podobny do ΔABO w skali		=		( DOC jest 4 razy mniejszy od ΔABO)
	8		4

P_ΔAOB=16*P_ΔDOC

	1
OC=		|OA|
	4

ΔCOB ma tę samą wysokość co ΔAOB⇒

	1		1
PΔCOB =		P {ΔAOB}=		*16*PΔDOC=4PΔDOC
	4		4

P_trapezu=4P_ΔDOC+4P_ΔDOC+P_ΔDOC+16P_ΔDOC=25P_ΔDOC 25P_ΔDOC=20

	4
PΔDOC=
	5

	4
PΔAOB=16*
	5

	4
PCOB=4*		=PΔDOA
	5

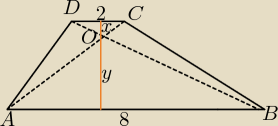
Mila: II sposób

	1
ΔDOC∼ΔAOB w skali
	4

x+y=4

x		1
	=
y		4

y=4x 4x+x=4 5x=4

	4		16
x=		i y=
	5		5

	1		4		4
PDOC=		*2*		=
	2		5		5

	1		16		64
PAOB=		*8*		=
	2		5		5

	1		64		16
PCOB=PDOC=		*		=
	4		5		5