okrąg wpisany w trapez Krzysiek2: na okręgu o danym promieniu r opisano trapez równoramienny ABCD o dluższej podstawie AB i

	|CK|
krótszej CD , punkt styczności K dzieli ramie BC tak ze		= 2/3
	|KB|

a) wyznacz dlugosc ramienia trapezu b) oblicz cos kata CBD

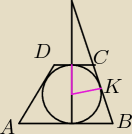♊: promień Zdaję mi się, że to zadanie na zastosowanie tw. Talesa, ale obliczenia będą nieciekawe. Może ktoś znajdzie lepszy sposób. Bo rozwiązanie tego z tw talesa zajmie ~50 minut na maturze.

Bogdan:

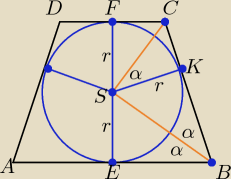
|CK|		2
	=
|KB|		3

	|CK|		r
Trójkąty CKS i BKS są podobne, stąd		=
	r		|KB|

Z układu równań:

	|CK|		2
1.		=
	|KB|		3

	|CK|		r
2.		=
	r		|KB|

obliczysz |CK| i |KB|, oraz potem |BC| = |CK| + |KB|

♊: Wiedziałem, ze jest prostrzy sposób :P

Tomek: Oby nie dali czegos takiego na maturze

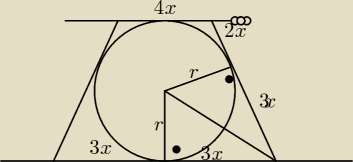Krzysiek2: Te dwa trójkąty są przystające, więc można napisać, że połowa dolnej podstawy to 3x, w sumie 6x, na dolną zostaje 4x(bo5x+5x=10x, a 10x−6x=4x). Teraz już wszystko banalnie proste, wynik −

	5r√6
		.
	6

Sorry, nie wiedziałem jak zmazać te kropeczki u góry