romb ***aga***: oblicz pole koła wpisanego w romb o boku dł 5 cm wiedząc że suma dł jego przekątnych jest równa 14 cm

Jakub: Podobne zadanie 1857

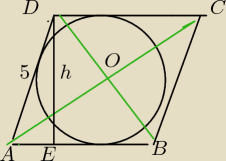
AS: Przypominam własność rombu: Przekątne się połowią i są do siebie prostopadłe. Zakładam: AC = c , wtedy BD = 14 − x Do ΔAOD stosuję tw. Pitagorasa (x/2)² + ((14 − x)/2)² = 5² |*4 x² + (14 − x)² = 100 x² + 196 − 28*x + x² = 100 2*x² − 28*x + 96 = 0 |:2 x² −14*x + 48 = 0 Δ = (−14)² − 4*1*48 = 196 − 192 = 4 , √Δ = 2 x1 = 6 (BD) , x2 = 8 (AC) Obliczam pole rombu a*h = 0.5*d1*d2 ⇒ 5*h = 0.5*6*8 ⇒ 5*h = 24 ⇒ h = 4,8 Wysokość h jest średnicą szukanego koła 2*r = h ⇒ r = h/2 ⇒ r = 2,4 Pole koła S = π*r² = 2,4²*π = 5,76*π