Funkcja kwadratowa.
MM: Naszkicuj wykres funkcji y= −x2 + 2x + 1 i napisz równanie osi symetrii jej wykresu.
23 paź 21:23
Mati_gg9225535:
policz sobie punkty charakterystyczne takie jak:
1. wierzchołek W=(p,q)
2. miejsca zerowe f(x)=0
3. punkt przecięcia z osią OY: A=(x,y)
to Ci ułatwi naszkicowanie wykresu,
a równanie osi symetrii jest to funkcja która przyjmuje postać x=p (pierwsza współrzędna
wierzchołka)
23 paź 21:26
MM: No właśnie z tym mam problem. Policzyłam wierzchołek i dwa miejsca zerowe, no i mój wierzchołek
nie jest tak jakby pomiędzy tymi miejscami zerowymi, tylko o jeden przesunął się do jednego z
miejsc zerowych. No i to dziwnie wygląda, bo zawsze jak rysowałam, to ten wierzchołek był
pomiędzy i było równe.
23 paź 21:30
Mati_gg9225535:
ewentualnie zastosuj wzór funkcji przekształcając go w postać kanoniczną, z której od razu
odczytasz współrzędne wierzchołka
f(x)= a(x−p)2+q
wtedy możesz rysować wykres dokonując przekształceń wykresu y=x2
1. y=x2
2. y= −f(x) − symetria względem osi OY
y=−x2
3. Tu=[p,q]
y=−(x−p)2+q
ten sposób wydaje się prostszy, ponieważ zauważyć można że funkcja dana w zadaniu może zostać
zwinięta wg wzoru skróconego mnożenia a2−2ab+b2=(a−b)2 wówczas ta postać jest postacią
kanoniczną
23 paź 21:31
Mati_gg9225535:
nie możliwe że jest przesunięty

popraw obliczenia

jesteś pewien że w zadaniu y= −x
2 + 2x + 1 ? sprawdź znaki
23 paź 21:34
aniabb: wierzchołek x=1
Δ=8
x1=1−√2 x2=1+√2 równo w połowie
23 paź 21:35
aniabb: yw=−8/−4=2
23 paź 21:36
pigor: ....np. tak :
y= −x
2+2x+1= −(x
2−2x)+1= −(x
2−2x+1−1)+1=
−(x−1)2+2, czyli
przesuń parabolę
y= −x2 o wektor
[1,2] , czyli o 1 w prawo i 2 w górę,:
oś symetrii otrzymanej po przesunięciu paraboli to prosta
x=1 . ...

23 paź 21:44
Eta:
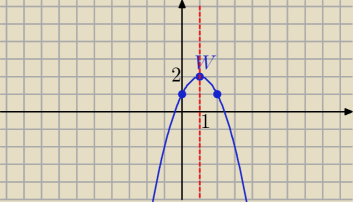
23 paź 21:54
łukasz: y=x2
11 wrz 15:24
 popraw obliczenia
popraw obliczenia  jesteś pewien że w zadaniu y= −x2 + 2x + 1 ? sprawdź znaki
jesteś pewien że w zadaniu y= −x2 + 2x + 1 ? sprawdź znaki

