geometria wykreślna
piórnik: Wiem , że to nie po to jest ta strona, ale jestem całkiem załamany. Może ktoś jest wstanie
pomóc mi z geometrii wykreślnej? takie podobno "proste" zadania? Jeśli tak to prosze o kontakt
i wrzuce treść
23 paź 20:11
ff: już dawno z tego nic nie robiłem − ale jeżeli proste to może dałbym radę − jakiego typu?
widoczność, przenikanie, kłady, obroty ?
23 paź 20:17
aniabb: jezeli na WAT to faktycznie proste były
23 paź 20:18
piórnik: ?
23 paź 20:32
piórnik: za chwile wrzuce i pomożecie?
23 paź 20:33
ff: spróbujemy(przynajmniej ja − do 22), nie wrzucaj może masowo − tylko tak na rozeznanie − czy
będziemy w stanie
23 paź 20:36
piórnik: okej to wrzuce 1

może chociaż podacie mi kroki co po kolei powinna zrobic
23 paź 20:38
piórnik:
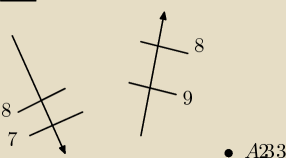
Zad 1.
Dane są płaszczyzny α oraz β a także punkt A. Przez punkt A poprowadź prostą l, która jest
równoległa do obu płaszczyzn.
23 paź 20:42
piórnik: oczywiście tam jest 8'α i 7'α, a przy strzałce s'α
a przy tym drugim jest z β
a punkt A ma (23,3)
23 paź 20:46
ff: ok, przy cechowanym to raczej ze mną cienko − liczyłem na bardziej abstrakcyjną gw,
pomyślę − ale niestety po mnie zbyt wiele nie oczekuj

23 paź 20:47
piórnik: mam jeszcze inne, gdzie tzeba wyznaczyć punkt przebicia. z takim dasz radę lepiej?
23 paź 20:49
ff: spróbujmy
23 paź 20:52
piórnik:
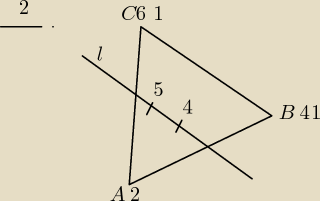
Dany jest rzut ΔABC oraz prostej l. Wyznaczyć punkt przebicia trójkąta (płaszczyzny określonej
przez wierzchołki trójkąta ) prostą l.
23 paź 20:56
piórnik: B'(4,1)
C'(6,1)
23 paź 20:57
ff: co do pierwszego: jeżeli prosta ma być równoległa do obydwu płaszczyzn − to będzie równoległa
do ich krawędzi przecięcia, punkty do krawędzi przecięcia uzyskasz na przecięciu poziomów 8' α
i 8' β, oraz 9' α i 9'β, potem rysujesz rzut prostej równoległej do rzutu krawędzi α i β i
zaznaczasz cechy tak, żeby przebiła rzut A
23 paź 20:57
ff: jakie wsp. ma A' ?
23 paź 21:03
ff: czegoś nie czaję − dlaczego dwie współrzędne?
23 paź 21:04
ff: nie jest tak, że ta druga liczba to numer płaszczyzny do której dany punkt przynależy?
23 paź 21:05
piórnik: A'(2) tylko tyle mam podane
23 paź 21:09
23 paź 21:11
ff: chyba, że jest to jedna współrzędna(liczba rzeczywista), np dla B: 4.1 − żeby świat nie był
taki piękny

23 paź 21:18
ff: jak z pierwszym? (rysunek nie chce mi się tu załadować)
23 paź 21:19
piórnik: aaaaa, możliwe ze tak jest
a umiesz mi pomoc z tym zadaniem?
23 paź 21:19
piórnik: właśnie rysuje sobie, ale chyba wiem o co chodzi już w tym pierwszym. tylko ta ostatnia część
zaznaczasz cechy tak, żeby przebiła rzut A niebardzo

23 paź 21:20
ff:
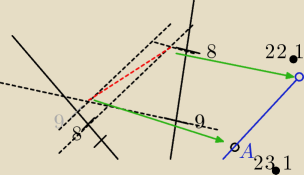
czerwona i niebieska − mająbyć równoległe, nachylenie prostej masz przez przeniesienie odcinka
(mamy jego spad z 9 na 8)
23 paź 21:22
ff: czy tam 23.3 to odpowiednio będzie 22.3
23 paź 21:23
piórnik: okej rozumiem to 1 dzięki ogromne

23 paź 21:31
piórnik: a napiszesz mi taki plan do 2? i prosiłabym najbardziej o pomoc z 4
23 paź 21:32
ff: w drugim to kombinowałbym tak, że w połowie CB uzyskamy punkt o cesze 3.1 − co nam daje skok o
1 jednostkę na płaszczyźnie tego trójkąta, teraz co dalej − możemy o ten skok przesunąć
dwójkę, ale czy to coś daje?
23 paź 21:36
piórnik: no właśnie tego drugiego to tez nie wiem

23 paź 21:37
ff: pomyłka: nie 3.1: 5.1 (ale liczy się, że mamy nachylenie)
23 paź 21:38
piórnik: to rozumiem
23 paź 21:43
ff: w 4 korzystamy z podpowiedzi

będzie potrzebne miejsce w lewym górnym rogu na kartce, żeby
znaleźć punkt przebicia
23 paź 21:46
piórnik: a nie opiszesz mi tego tak krok po kroku ?
23 paź 21:47
ff: rysunek się mi znów ładuje − ale do tego czasu − kojarzysz sposób na znalezenia punktu
przebicia płaszczyzny prostą? (bo ja jak przez mgłę)
23 paź 21:52
ff:
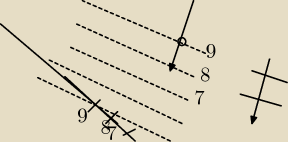
jednak nie lewym górnym rogu − tylko niestety nie kojarzę zbytnio jak szukało się przebicia
prostą płaszczyzny?
23 paź 21:53
ff: za duży spadek narysowałem, żeby w ogóle go szukać − jeszcze raz
23 paź 21:54
piórnik: niestety tego przebicia w ogóle nie kojarze

23 paź 21:56
23 paź 22:06
ff: chyba mam − dwie proste równoległe wyznaczają płaszczyznę, prowadzimy prostą równoległą do l
przechodzącą przez A − otrzymujemy jakąś γ, znajdujemy krawędź płaszczyzny β i γ, przecięcie
rzutu tej krawędzi z rzutem l to będzie punkt przebicia − jeżeli dobrze kojarze − spróbuję to
narysować
23 paź 22:11
piórnik: jestes wspaniały

!
23 paź 22:16
ff:
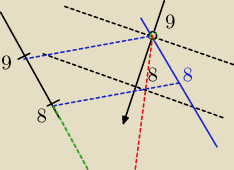
chyba tak: prowadzę prostą równoległą do l przez A (niebieska ciągła) − otrzymuję płaszczyznę
(niebieska przerywana) − znajduję krawędź tych płaszczyzn (czerwona przerywana) to punkt
przebicia będzie na przedłużeniu krawędzi płaszczyzn i prostej l
ale to musisz jeszcze przemyśleć − bo mogę się mylić
23 paź 22:24
piórnik: okej dzieki wielkie, dopytam się jutro i pomyśle

nie wiem jak ci się odwięcze
23 paź 22:28
ff: no problemo − była polsl pozdrawia

23 paź 22:31
piórnik: pozdrawiam i dziekuje za pomoc
23 paź 22:37
 może chociaż podacie mi kroki co po kolei powinna zrobic
może chociaż podacie mi kroki co po kolei powinna zrobic
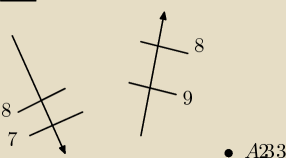 Zad 1.
Dane są płaszczyzny α oraz β a także punkt A. Przez punkt A poprowadź prostą l, która jest
równoległa do obu płaszczyzn.
Zad 1.
Dane są płaszczyzny α oraz β a także punkt A. Przez punkt A poprowadź prostą l, która jest
równoległa do obu płaszczyzn.

 Dany jest rzut ΔABC oraz prostej l. Wyznaczyć punkt przebicia trójkąta (płaszczyzny określonej
przez wierzchołki trójkąta ) prostą l.
Dany jest rzut ΔABC oraz prostej l. Wyznaczyć punkt przebicia trójkąta (płaszczyzny określonej
przez wierzchołki trójkąta ) prostą l.


 czerwona i niebieska − mająbyć równoległe, nachylenie prostej masz przez przeniesienie odcinka
(mamy jego spad z 9 na 8)
czerwona i niebieska − mająbyć równoległe, nachylenie prostej masz przez przeniesienie odcinka
(mamy jego spad z 9 na 8)


 będzie potrzebne miejsce w lewym górnym rogu na kartce, żeby
znaleźć punkt przebicia
będzie potrzebne miejsce w lewym górnym rogu na kartce, żeby
znaleźć punkt przebicia
 jednak nie lewym górnym rogu − tylko niestety nie kojarzę zbytnio jak szukało się przebicia
prostą płaszczyzny?
jednak nie lewym górnym rogu − tylko niestety nie kojarzę zbytnio jak szukało się przebicia
prostą płaszczyzny?

 !
!
 chyba tak: prowadzę prostą równoległą do l przez A (niebieska ciągła) − otrzymuję płaszczyznę
(niebieska przerywana) − znajduję krawędź tych płaszczyzn (czerwona przerywana) to punkt
przebicia będzie na przedłużeniu krawędzi płaszczyzn i prostej l
ale to musisz jeszcze przemyśleć − bo mogę się mylić
chyba tak: prowadzę prostą równoległą do l przez A (niebieska ciągła) − otrzymuję płaszczyznę
(niebieska przerywana) − znajduję krawędź tych płaszczyzn (czerwona przerywana) to punkt
przebicia będzie na przedłużeniu krawędzi płaszczyzn i prostej l
ale to musisz jeszcze przemyśleć − bo mogę się mylić
 nie wiem jak ci się odwięcze
nie wiem jak ci się odwięcze
