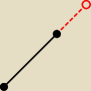
wyznaczenie współrzędnych punktu C powstałego po przedłużeniu odcinka o r slash851: Witam, proste zadanie ale nie mogę sobie z nim poradzić w trywialny sposób. Wydaje mi się że próbuje je rozwiązać zbyt skomplikowanie. Problem to wyznaczenie współrzędnych punktu [b]C[/b] po przedłużeniu prostej [b]AB[/b] o odcinek długości [b]r[/b] (zaznaczony na rysunku na czerwono i tworzący odcinek BC) wiadomymi są punkt A(x,y), B(x,y) oraz długość odcinka r Wymyśliłem 2 sposoby rozwiązania tego: 1. wyznaczam równanie prostej przechodzącej przez AB potem w punkcie B tworze okrąg o promieniu r i szukam punktów przecięcia prostej z okręgiem. Jeden z punktów jest punktem C 2. obliczam długość odcinka AB ze wzoru na odcinek. Obliczona długość odcinka + r daje mi długość odcinka AC. Mając długość odcinka AC podstawiam do wzoru [tex]AC = \sqrt{(xc−xa)²+(yc−ya)²}}[/tex] jedyne niewiadome to xc oraz yc które można stąd wyliczyć proszę o pomoc czy da się to rozwiącać w jakiś prostrzy sposób

kylo1303: Tzn mozna ukladem rownan: okresl wzor prostej y=Ax+B, twoj punkt C bedzie mial wspolrzedne (x, Ax+B). Czyli masz znalezc jeszcze jedno rownanie, np. odcinek BC=r.