W trapezie równoramiennym jedna z podstaw jest dwa razy dłuższa Natalia: 1. W trapezie równoramiennym jedna z podstaw jest dwa razy dłuższa od drugiej, a przekątna trapezu dzieli kąt przy dłuższej podstawie na połowy. Oblicz długość boków trapezu wiedząc, że jego pole jest równe 3√3 Do zadania wykonaj rysunek, zapisz wszystkie obliczenia i uzasadnienia.

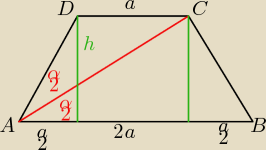
+-: Spróbuj dalej sama. Wsazówka oblicz h w funkcji α, oraz α/2 i wylicz α

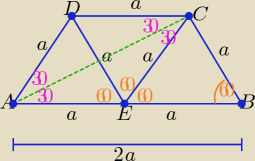
Eta: Można też tak taki trapez składa się z trzech przystających trójkątów równobocznych o boku długości "a" P(trapezu)= 3*P(Δrównobocznego)

	a2√3
3*		= 3√3 ⇒ ........... a=2
	4

+-: Wypadałoby wykazać, że są to trójkąty równoboczne.

Eta: W czym problem? Parę słów komentarza i koniec dowodu

+-: Eta masz rację,ale chciałbym zobaczyć komentarz od "Natalia", choć osobiście wątpię, "że będzie miał(a) czas".

Myk: Niestety to jest nie uzasadnione, nie można sobie od tak przyjmować, że kąty będą mieć 30 stopni, poza tym nie wyjaśnione jest jak powstaje kąt DEC.