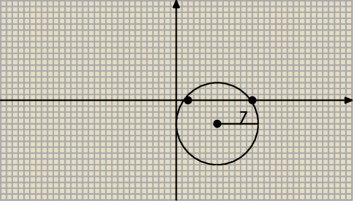
ocena Wątroba: Sprawdź, ile punktów wspólnych ma okrąg o równaniu (x−7)² + (y+4)² = 49 z osią rzędnych a ile z osią odciętych. czyli: (x+7)² + (y − (−4))² = √49 (7,4) , r = 7 I teraz nie wiem czy rysunek, który wykonałem jest prawidłowy względem tego zadania. Okrąg ma 2 punkty wspólne z osią ox. A z osią oy 1 ? Bo moze wyda sie to prymitywne ale mam wrazenie ze 2 pkt. Bo nachodzi na −4 i −5 na osi y. Poprostu napiszcie odpowiedz jesli znacie i bardzo dziekuje za uwage i czas

Wątroba: Rzuccie tylko okiem

Wątroba: Nikt sie nie podejmie?

ICSP: z osią odciętych − dwa z osią rzędnych − 1

Skipper: OK −

aniabb: skoro r = x środka to MUSI mieć 1 punkt , a że rysunek niestaranny ...

Wątroba: Niestaranny? W takim razie jak mam go wykonac zeby byl w miare dobry?

ICSP: mi tam się podoba Ważne że widać dokładnie ile jest punktów przecięć

aniabb: ostrym ołówkiem w cyrklu na papierze milimetrowym

Nieuk: CHodzi mi o ten wykonany tutaj. Jest slabo czytelny?

aniabb: albo do równania zamiast x wstawić 0 i policzyć ile y wychodzi a potem zamiast y wstawić 0 i policzyć jakie są x

Nieuk: mu*

Ajtek: Zamiast bawić się w rysowanie, można to zrobić algebraicznie. Witam aniabb, ICSP .

Wątroba: Musi być rysunek.. Niestety

ICSP: Witaj Ajtku Nie ma co robić r = 7 S(7;−4) zatem odległość od osi OX = 4 < r − dwa punkty oraz odległość od OY = 7 = r − jeden punkty. Tyle z zadania

Wątroba: O kurde, narysowalem po zlej stronie te kolko. fakt, tam ma byc −4

Ajtek: Ty to wiesz, aniabb to wie, ja rónież to wiem. Ale uczniowie mogą tego nie zauważać po pierwszym spojrzeniu na wzór okręgu.

aniabb: ja nic nie wiem ja tu tylko sprzątam

Wątroba: Ale jak juz nie bede tego ruszal to bedziwe dobrze? Moge to przepisac do zeszytu? Tak jak jest

ICSP: Możesz przesiać Rysunek też masz ładny

Ajtek: Tylko nie ta współrzędna po x jest .

aniabb: ale to On osobiście tam widział nieskończenie wiele punktów wspólnych ..