okrąg, styczne imię lub nick: dany jest okrąg o równaniu x²+y²+6x−4y=12. wyznacz równianie stycznych do okręgu

	1
prostopadłych do prostej l: y=		x−5
	3

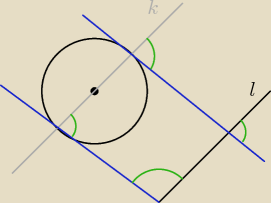
♊: Kąty zaznaczone na zielono mają miarę 90^o Prosta k ∥ l Niebieskie linie to te styczne, co to masz je wyznaczyć.

♊: Już wiesz jak to rozwiązać ? ;>

joanna: aby znależć punkty styczności rozwiązujesz układ

	1
x2+y2+6x−4y=12 i y=		x−5 czyli do pierwszego zamiast y podstawiasz drugie
	3

joanna: głupoty gadam

joanna: od początku

joanna: moment

imię lub nick: wyznaczam prostą przechodzacą przez środek okrędu i prostopadłą do l, następnie punkt przecięcia z l, dwa punkty odległe o r od punktu przecięcia na prostej l i proste prostopadłe do prostej l przechodzące przez te punkty?

imię lub nick: a może proste odległe od środka okręgu o r protopadłe do l, tak z bomby. da się tak?

Darek: ja mam inny pomysl, nie wiem czy slusznie rozumuje, jakby ktos mogl przejrzec i potwierdzic : wpierw to bym zrobil se ino wzor na to kółko x²+y²+6x−4y=12 (x+3)² + (y−2)² = 25 wiec mamy kolko o S= (−3, 2) i r−5 (r napewno sie przyda, do okreslenia odleglosci ) mamy wyznaczyc jakies proste p i q ktore sa prostopadle do l ( p i q sa tymi szukanymi stycznymi) p ⊥ l : y= −3x+b −−> 3x +y +b = 0 (q jest takie same, z tymze bedzie −b ) 1 styczna przechodzi przez P, druga przez Q (jak zwal, tak zwal ), które są równo oddalone od S (srodka kolka ) wzor na odleglosc prostej od punkta:

	Ax0+By0+C
d=
	√A2+B2

a wiec dane : prosta: 3x +y +b = 0 ; A=3, B=1, C=b punkt : S=(−3, 2) ; x₀=−3; y₀=2 i d = r, wiec d = 5

	−9+2+b
5=
	√10

5√10=−7+b b=5√10+7 a wiec d = 5 istnieje dla b = 5√10+7 bo drugie jest −b, mozna rozwiazac

	Ax0+By0−C
d=
	√A2+B2

wiec wg mnie te styczne to: p: y=3x + 5√10+7 q: y=3x − 5√10−7 −−−−−−−−−−−−−− moze ktos przeanalizowac moje podejscie do zadania

joanna: przekształcamy równanie okręgu (x+3)²−9+(y−2)²−4=12 (x+3)²+(y−2)²=12+13 (x+3)²+(y−2)²=5² S=(−3,2), r=5 równanie stycznej ma ogólną postać (x−a)(x₁−a)+(y−a)(y₁−a)=r²

joanna: chyba słusznie darku

joanna: (a,b)=S=(−3,2) y₁=−3x₁+b z warunku prostopadłośi o którym pisał Darek

♊: imię lub nick − wg mojego oznaczenia, to powinno wyglądać tak: ___________________________________________________________________________ wyznaczam prostą przechodzacą przez środek okrędu i prostopadłą do l, następnie punkt przecięcia z k, dwa punkty odległe o r od punktu przecięcia na prostej k i proste prostopadłe do prostej k* przechodzące przez te punkty? ___________________________________________________________________________ * tam przy ostatnim może być za równo k jak i l :P imię lub nick − znając odpowiednie wzory to pewnie tak, ja, z moja wiedzą o geometrii analitycznej bym liczył moim sposobem :P

Darek: wlasnie to "chyba" tez mnie boli ja to widzialem jakos tak, i nie wiem czy jak te "r" nie sa równoległe do O_y to ja se ot tak w drugiej prostej przyjac b jako −b tej prostej wyzej

imię lub nick: ♊ − Twój sposób jest najłatwiejszy. wyznaczyć k jako równoległą do l przechodzącą prze środek, punkty przecięcia z okręgiem i potem już łatwo... dzięki wszystkim za pomoc.

♊: Narysowałem 3 przykładowe możliwości otrzymanych prostych przez Ciebie Darku. We wszystkich przypadkach (zaznaczone kropki to przykładowe P i Q, linie to p, q). Wszystkie są równoodległe od środka okręgu i wszystkie są prostopadłe do l. Jaką masz pewność, że otrzymałeś popawne (u mnei − niebieskie) proste ? Bo tego chyba w Twoim zadaniu brakuje (albo przeoczyłem). Nie widzę założenia, że proste są w odległości r od środka okręgu (tylko, ze przecodzą przez punkty w odleglości r, a takich przypadków jest nieskończenie wiele).

Darek: no tez sie tego obawialem i musze sie z Toba zgodzic tez chcialem robic uklad rownan podstawiajac y ... ale te kwadraty w ulamakch ... grr wyjasniles mi dokladnie moj blad xd ladny obrazek

♊: Żeby zrobić poprawnie to zadanie musiałbyś wziać pod uwagę, że P i R należą do prostej równoległej do l (czyli wyznaczyć prostą k z "mojego" sposobu). To natomiast byłoby bardziej złożoną obliczeniowo wersją mojej metory, więc nieopłacalne na maturze. Właśnie od tego tu jestem by zwracać uwagę na błędy, za jakei można stracić punkty na maturze (no i od tego, by podpowiadać jak rozwiązać zadania których nie potraficie ;P)

Darek: czyli w sumie Ty: 1. wyznaczylbys prosta k równoległa do l i przechodzaca przez S 2. nastepnie czesc wspolna K i okregu (do wyznaczenia pkt stycznosci tych stycznych xd) 3. i majac pkt stycznosci 2 proste, przechodzace przez te 2 punkty (2 punkty, 2 proste) i ⊥ do prostej l dobrze zrozumialem ^^

♊: Tak. Dokładnie tak bym zrobił.

Darek: krok I: k || l : y= ¹₃x+b i k przechodiz przez S = (−3,2) 2=−1+b b=3 krok II: buuu (to bedzie be ) x²+y²+6x−4y=12 y= ¹₃x+3 x²+(¹₃x+3)²+6x−4(¹₃x+3)=12 x²+¹₉x²+2x+9+6x−⁴₃x+12=12 ¹⁰₉x²+²⁰₃x+9=0 10x²+60x+81=0 Δ=3600−3240=360 √Δ=6√10

	−60−6√10		−60+6√10
x1=		x2=
	20		20

	2(−30−3√10)		2(−30+3√10)
x1=		x2=
	20		20

	−30−3√10		−30+3√10
x1=		x2=
	10		10

x₁=−3−^3√10₁₀ x₂=−3+^3√10₁₀ y= ¹₃x+3 y₁= ¹₃ * (−3−^3√10₁₀) +3 y₁=−1−^√10₁₀ +3 ^√10₁₀ = 10^−1₂ x₁=−3−3*10^−1₂ x₂=−3+3*10^−1₂ y₁=2−10^−1₂ y₂=2+10^−1₂ jak narazie cos takiego xd jeszcze krok 3ci

Darek: krok III pr styczne ⊥ l : y=−3x+b 1sza prosta: 2−10^−1₂= −3 (−3−3*10^{−¹₂) +b 2−10^{−¹₂ = 9 +9 * 10^{−¹₂ +b −19^{−¹₂ −7 = b ta prosta jest ble 2ga : 2+10^−1₂= −3 (−3+3*10^{−¹₂) +b 2+10^{−¹₂ = 9 −9 * 10^{−¹₂ +b 19^{−¹₂ −7 = b tez ble xd takie mzoe byc rozwiazanie czy to raczej ... jakis babol ^^ bo mnie sie nie podoba

♊: Ja bym zapisał zamiast tej potęgi −½ może jakoś inaczej ? No nie wiem . . . pierwiastek jakiś ?

♊: Ale obliczenia sprawdzę później bo teraz wykład . . . ;P

♊: A to nie powinno być tak ? Wtenczas jest mniej ble . . .

	1		1
2−√(		) = 9 + 9 * √(		) +b
	10		10

	1		1
2−9 − √(		) − 9 * √(		) = b
	10		10

	1		1
2−9 − 1* √(		) − 9 * √(		) = b
	10		10

	1
−7 − 10 √(		) = b
	10

	√1
−7 − 10		= b
	√10

	1
−7 − 10		= b
	√10

	10*1
−7 −		= b
	√10

	10
−7 −		= b
	√10

	√100
−7 −		= b
	√10

	100
−7 − √(		) = b
	10

−7 − √10 = b

Darek: o O.o a na taki rozklad to ja nie wpadlem a i swoaj droga, to ejdnak to "b" jest takie same jak tamto b wyyyyyzej te duuzo wyzej xd

♊: i dodatkowo to co mi wyszło 10 * √10^½ Ty zapisałeś jako 19 * √10^½ ;P Nie wiem o które b i które wyżej i bardziej wyżej Ci chodzi, ale zapewne masz rację ;P

♊: Znaczy się teraz w tej mojej ostateniej wiadokości powinno być 10⁻¹ pod pierwiastkiem a nie ^½

Darek: musialem sie pomylic w obliczenaich xd a o b chodiz mi to co robilem metoda na ktora wpadlem za pierwszym razem 10ty post od gory

♊: tam masz 5√10 + 7 a tu 1 √10 − 7 więc ja widze pewne różnice . . . Aha − lepszym określeniem jest data i godzina przy poście niż x podzycja licząc od y w górę lub w dół :p

Darek: a rzeczywiscie zle spojrzalem a na godzine nei wpadlem ^^ spamik ale i tak wynik mialbym podobny

♊: tak . . . podobny

Darek: jakby bylo na maturze starcilbym ... tylko .... kilka ... pkt mozeby kto nei zauwazyl roznocy ... mozna obliczyc prawdopodobienstwo, xd tworze zadanie: matury sprawdza (podobno ) 3 specjalistow. Oblicz prawdopodobienstwo, ze cala trojka nie zobaczy bledu