pochodne, zadania, pomoc
ohayou: 1.Uzasadnij, że równanie posiada dokl. jedno rozwiazanie:
2.Oblicz kąt pod którym przecinają się wykresy
f(x)=e
x
g(x)=e
−√3x
W tym drugim zdaje się muszę policzyć styczne do tych wykresów ze wzoru y−f(x
o}=f'(x
o)(x−x
o)
więc liczę pochodną pierwszego a więc końcowo z f(x) wychodzi y=ex
drugi wykres to funkcja złożona f(x) i jakieś c(x)=−
√3x... z tego mi wyszło y=−
√3e
y ,
chociaż nie jestem pewny czy to dobrze

i nie za bardzo wiem, co dalej. Pomoże ktoś?
Godzio:
Zadanie 1
| | 1 | |
Zdefiniujmy funkcję f(x) = ex − |
| |
| | x | |
| | 1 | |
Sprawdźmy co się dzieje na przedziale [ |
| , 1] |
| | 10 | |
f(1) = e − 1 > 0
| | 1 | |
f( |
| ) = e1/10 − 10 < 0 |
| | 10 | |
Ponadto
| | 1 | |
f'(x) = ex + |
| > 0 dla x ∊ R − {0} |
| | x2 | |
Zatem funkcja jest cały czas rosnąca, więc nigdy nie przetnie osi OX 2 razy,
Z własności Darboux oraz z rośnięcia funkcji wnioskujemy, że istnieje dokładnie jedno
rozwiązanie.
 i nie za bardzo wiem, co dalej. Pomoże ktoś?
i nie za bardzo wiem, co dalej. Pomoże ktoś?
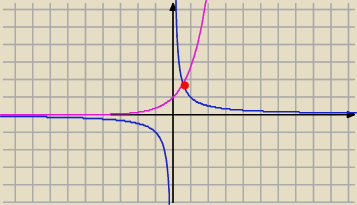 1) rozwiąż graficznie.
1) rozwiąż graficznie.
 ale trzeba mi mocniejszego dowodu algebraicznego, czy na pochodnych..
eh.
ale trzeba mi mocniejszego dowodu algebraicznego, czy na pochodnych..
eh.