Czworokąt ABCD wpisany jest w okrąg. Kaś;*: Czworokąt ABCD wpisany jest w okrąg. Proste zawierające boki AB i CD przecinają się w punkcie K. Oblicz ile razy bok AB jest dłuższy niż bok CD jeśli punkt B jest środkiem odcinka AK i stosunek DC do CK jest równy 1:8

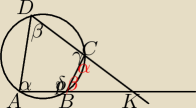
joanna: ponieważ czworokąt jest wpisany w okrąg to α+γ=180 i β+δ=180 stąd γ=180−α i δ=180−β kąt BCK = 180−γ=α kąt CBK=180−δ=β wiadomo że AB:BK=1:1 stąd przyjmijmy że AB=x=BK natomiast DC:CK = 1:8 więc niech DC=y zaś CK=8y mamy DK=9y oraz AK=2x dla trójkąta AKD z twierdzenia sinusów:

	2x		9y
(1)		=
	sinβ		sinα

zaś dla trójkąta BCK z tw sinusów:

	x		8y
(2)		=
	sinα		sinβ

	2xsinα
z (1) mamy sinβ=		i wstawiając do (2) otrzymujemy
	9y

8y*9y		x
	=		(...)
2xsinα		sinα

72y²−2x²=0 2(6y−x)(6y+x)=0 stąd x=6y lub x=−6y (sprzeczne) więc AB=x=6y, DC=y i ostatecznie

AB		6y
	=		=6
DC		y

odp. Bok Ab jest 6 razy dłuższy niż DC