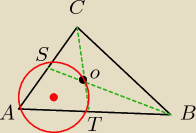
Dwusieczna kąta przy wierzchołku B w ΔABC Kaś;*: Dwusieczna kąta przy wierzchołku B w ΔABC przecina bok AC w punkcie S,a dwusieczna kąta C przecina bok AB w punkcie T. Dwusieczne te przecinają sie w punkcie O. Znajdź miare kąta α jeśli wiadomo, że na czworokącie ATOS można opisać okrąg.

Krzysiek: kat α to kat przy wierzcholku A tak

Kaś;*: tak α jest przy wierzchołku A, ale jak obliczyć jego miare, jak nie ma danych

Kaś;*: a tak wogóle to dzieki za odpowiedź

Eta: Witampodpowiem; oznaczmy kąty przy A −−− jako 2α przy B −−− jako 2β przy C −−− jako 2γ to 2α+2β+2γ= 180^o ( bo suma kątów trójkąta ABC więc α+β+γ= 90^o => β+γ= 90^o − α w trójkącie BOC kąt BOC = 180^o − ( β+γ) => że kąt BOC= 180^o − 90^o +α zatem <BOC= 90^o +α kąt ten jest równy kątowi TOS −−−− jako kąty wierzchołkowe ponieważ na czworokacie ATOS można opisać okrąg : to sumy kątów przeciwległych są równe i mają miarę 180^o więc : 2α + <ATOS = 180^o => 2α + 90^o +α= 180^o więc 3α= 90^o => α= 30^o to kąt A=2α = 60^o