Fajne Archimonde: Rozwiąż równanie: x²−6x+2|x−3|−|x+1|+13=0

sushi_gg6397228: musisz pozbyc sie wartosci bezwzglednej

Archimonde: co ty jak na to wpadłeś?

sushi_gg6397228: rzuciłem monetą i wypadło na kant https://matematykaszkolna.pl/strona/1796.html

Archimonde: Oj jak masz tak pomagać to lepiej wcale nie pomagaj.

Archimonde: umie to ktoś zrobić?

Archimonde: ej

Archimonde: ludzie

Mila: x²−6x+2|x−3|−|x+1|+13=0 1) x−3≥0⇔x≥3 2) x+1≥0⇔x≥−1 rozważam równanie w przedziałach: a) x<−1 obydwa wyrażenia są ujemne [ (x−3)<0 i (x+1)<0] mamy rownanie x²−6x+2(−x+3)−(−x−1)+13=0 x²−6x−2x+6+x+1+13=0 x²−7x+20=0 Δ=49−4*20<0 brak rozwiązań b)x≥−1 i x<3 x²−6x+2(−x+3)−(x+1)+13=0 x²−9x+18=0 Δ=9

	9−3		9+3
X1=		lub x2=
	2		2

x₁=3 lub x₂=6 obydwa nie należą do dziedziny rownania c)x≥3 x²−6x+2(x−3)−(x+1)+13=0 x²−6x+2x−6−x−1+13=0 x²−5x+6=0 Δ=1

	5−1		5+1
x1=		lub x2=
	2		2

x₁=2 nie należy do przedziału lub x₂=3∊D odp. x=3

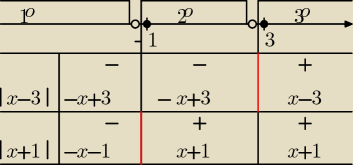
Gustlik: Metoda "osi i tabelki": x²−6x+2|x−3|−|x+1|+13=0 Układam te 3 przypadki kolumnami: 1^o) x²−6x+2(−x+3)−(−x−1)+13=0, zał. x∊(−∞, −1) 2^o) x²−6x+2(−x+3)−(x+1)+13=0, zał. x∊<−1, 3) 3^o) x²−6x+2(x−3)−(x+1)+13=0, zał. x∊<3, +∞) Rozwiąż teraz te 3 przypadki i uwzględnij tylko te pierwiastki, które spełniają założenia dla danego przypadku.