parametr Saizou : Oblicz dla jakiej wartości m zbiór rozwiązań nierówność x²−3x+2<0 jest zawarty w zbiorze rozwiązań nierówności x²−(2m−1)x−2m>0 i otóż ja wyliczyłem x²−3x+2<0 i wychodzi x∊(1:2) policzyłem również Δ=(2m+1)² dla x²−(2m−1)x−2m>0 oraz obliczyłem pierwiastki tego czegoś x₁=−1 (pierwiastek stały, który się nie zmienia od parametru m) x₂=2m

	1
i stwierdziłem że 2m<1→m<
	2

i pytanie czy wystarczy coś takiego napisać

Maslanek: Nie. Najlepiej rozważ przypadek, kiedy zbiór tamtej nierówności nie jest zawarty w zbiorze rozwiązań tej. Będzie prościej

Maslanek: Chociaż w sumie... Ale to i tak powinieneś zrobic 2m>1 i odjąć to od zbioru głównego.

Saizou : no ale jeżeli m>0,5 to zbiór pierwszej nierówności nie będzie zwarty w drugim

Maslanek: Tak

	1
Ale: m≤
	2

Saizou : taki chochlik przy przepisywaniu

Saizou :

Saizou : up

Maslanek: Nie no ok

Eta: Echhh ........ sorry źle przeczytałam treść zadania ( zaraz to wykasuję) Myślę,że już teraz sam dopasujesz odpowiednie warunki ... co?

Saizou : a czy to co ja napisałem jest OK, z całym szacunkiem dla Maslanka ale wiesz im więcej na Tak tym lepiej

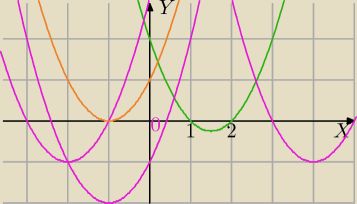
Mila: Rozważ te różowe przypadki.

Mila: Δ≥0 dla każdego m∊R

	−1
1) Δ=0⇔2m+1=0⇔m=
	2

wówczas g(x)=x²−(2m−1)x−2m ma postać: g(x)=x²+2x+1=(x+1)² wykres pomarańczowy i (1;2) zawiera się w zbiorze rozwiązań nierówności (x+1)² >0 2)Δ>0 i x_w>2 i f(2)≥0 3) Δ>0 i x_w<1 i f(1)≥0