Zadanie maturalne Damian: W środę zdaję maturę...więc bardzo bym prosił o wytłumaczenie mi jednego zadanka... :−) w zadaniach z wartością bezwzględną typu |x−2| + |3x−6| < |x| W rozumowaniu ma "przedziały" skąd wiadomo w jakim przedziale dać jaki znak, chodzi o < i >, ≤ i ≥

Krzysiek: sluchaj damian

Krzysiek: ja tez zdaje

Krzysiek: w takich zadaniach to sie tak postepuje

Krzysiek: juz pisze:

♊: Nie ma to jak jedną wypowiedź rozwalić na 5 postów . . .

Damian: Czekam z niecierpliwością

Squall: | | nie czepiaj się chce chłopak pomóc to daj mu się wykazać

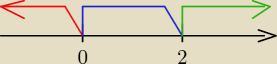
Krzysiek: np w tym przykladzie co ty dales to bedzie tak ze da sie wyciagnac 3 z drugiego modulu: |x−2| + |3x−6| < |x| ⇒ |x−2| + 3|x−2| − |x| < 0 ⇒ 4|x−2|−|x| < 0 to nieco uprosci sprawe i teraz jesli chodzi o te znaki to ja sobie zawsze przyjmuje tak: rysuje sobie taka os i zaznaczam przedzialy jak na rysunku ( dla tego przypadku ) i masz: dla x ε (−∞,0) nierownosc przyjmuje postac −4x+8+x<0 dla x ε <0,2) nierownosc przyjmuje postac −4x+8−x<0 dla x ε <2,+∞) nierownosc przyjmuje postac 4x−8−x<0 rozwiazujesz powyzsze przypadki; w kazdym z trzech przypadkow bierzesz czesc wspolna zalozenia dla przypadku i nierownosci w danym przypadku powinny ci wyjsc z tego jakies trzy przedzialy i teraz bierzesz sume tych przedzialow i to jest koncowa odpowiedz mam nadzieje ze to mniej wiecej zrozumiale

Krzysiek: Squall bujaj wroty mam nadzieje ze dobrze napisalem

Krzysiek: ale to od ciebie zalezy jak sobie przyjmiesz gdzie przedzial domkniety a gdzie otwarty bylebys tylko potem rozwiazal w tych przedzialach co sobie przyjales

C: Damian jaki poziom zdajesz?

Krzysiek: pewnie rozszerzony

Damian: aha Już wszystko się wyklarowało Zdaję podstawę Wielkie dzięki za pomoc

Krzysiek: skoro sie wyklarowalo to okej

Krzysiek2: |x−2|+3|x−2|<|x| 4|x−2|<|x| przedziały: (−∞;0) , <0;2) , (2;+∞) dla kolejnych przedziałów podstawiasz to x z przedziałów do wartości bezwzględnych i wychodzi, że: dla x∊ (−∞;0) x−2<0, więc |x−2|=−x+2 x<0, więc |x|=−x −3x+8<0 −3x<−8

	3
x>		, ale on nie spełnia założeń przedziału, więc tu nie ma rozwiązań
	8

dla x∊<0;2) x−2<0, więc |x−2|=−x+2 x≥, więc |x|=x −5x+8<0 −5x<−8

	8		8
x>		tutaj spłenia nam iloczyn obu przedziałów, czyli x∊(		;2)
	5		5

dla x∊<2;+∞) x−2≥0, więc |x−2|=x−2 x>0, więć |x|=x 3x−8<0 3x<8

	3
x<		tutaj również nie ma rozwiązań.
	8

	8
Rozwiązaniem jest x∊(		;2) Jednak gdzies musiałem zrobić błąd, bo 2 też jest rozwiązaniem
	5

a u mnie go nie ma

Krzysiek: pozdro

AS: Podstawowa zależność x dla x > 0 jeżeli x = 7 to | x | = 7 |x| = 0 dla x = 0 jeżeli x = −7 to | x | = 7 albo −x (bo −(−7) = 7) −x dla x < 0 przykładowo dla |x − 2| W myśl poprzedniego |x − 2| = x − 2 dla x > 2 (2 miejsce zerowe) |x − 2| = −(x − 2) dla x < 2 Sprawdź dla x = 5 |x − 2| = |5 − 2| = 3 czuli tyle samo co x − 2 = 5 − 2 = 3 dla x = −11 |x − 2| = |−11 − 2| = |−13| = 13 czyli tyle samo co −(x − 2) = −(−11 − 2) = 13 Przykład przez Ciebie podany nie jest zbyt dobry Przykład: | x − 2| + |3*x − 13| > |x| Miejsca zerowe to: 0 , 2 , 13/3 Rozpatrzyć należy przedziały: (−∞,0) , 0 , (0,2) , 2 , (2,13/3) , 13/3 , (13/3,∞) Dla elementu z pierwszego przedziału np. −10 wyrażenia x − 2, 3*x − 13 , x przyjmują wartości ujemne Opuszczam znaki wartości bezwzględne i każde z nich poprzedzam znakiem " − " −(x − 2) − (3*x − 13/3) > −x => −4*x + 19/3 > −x Dla przedziału (o,2) wybieram x = 1 wtedy wartości x − 2 i 3*x − 13 są ujemne a x dodatnie Zapis będzie następujący −(x − 2) − (3*x − 13/3) > x => −4*x + 19/3 > x dla x =20 (x − 2) + (3*x − 13/3) > x => 4*x − 19/3 > x Podsumowanie Jeżeli dla wybranego x wyrażenie zawarte w wartości bezwzględnej przyjmuje wartość dodatnią to wyrażenie przepisujemy bez zmiany, opuszczając znaki wartości bezwzględnej. Jeżeli dla wybranego x wyrażenie zawarte w wartości bezwzględnej przyjmuje wartość ujemną to wyrażenie przepisujemy poprzedzając znakiem " −" opuszczając znaki wartości bezwzględnej.

Damian: Widze ze ktoś z moim nikiem zasiada na forum prosiłbym o jego delikatną zmiane z góry dzieki