@asdf bezendu1990: witam mam problem zadanie brzmi rozwiąż układ nierówności.

	x−1
−1<		<1
	x+1

x−1
	−1<0 Df=x∊R/{−1}
x+1

x−1−(x+1)
	<0
x+1

x−1−x−1
	<0
x+1

−2
	<0
x+1

−2(x+1)<0 x=−1 x∊(−∞,−1)

x−1
	>−1
x+1

x−1
	+1>0
x+1

x−1+x+1
	>0
x+1

2x
x+1

2x(x+1) x=0 x=−1 x∊(−∞.−1)∪(0,∞) A∪B=(−∞,−1)u(0,∞) A∩B=∅ A/B=∅ B/A=(0,∞) i z odpowiedzi wiem że to jest rozwiązaniem B/A=(0,∞) ale na maturze nie będę mial odpowiedzi wiec skąd mam wiedzieć który przedział będzie dobry

bezendu1990: @asdf pomożesz ?

Aga1.: Popraw −2x−2<0 −2x<2 x>−1 Znajdujesz część wspólną pierwszego i drugiego rozwiązania.

bezendu1990: ok dzięki

bezendu1990: ale wtedy będę miał ze zbiór a (−1,∞) to nie wyjdzie bo odpowiedź powinna wyjść (0,∞)

pigor: ... no właśnie, tak jak ty robią "matematyczni masochiści" i jest taki Pan na tym F. który tak właśnie Was uczy , bo ma dar od ... "alleluja i do przodu" , no i wszystko wie najlepiej , a ja pokażę np tak : −1< ^x−1_x+1 <1 ⇔ | ^x−1_x+1 |<1 /*|x+1|≠0 ⇔ |x−1|<|x+1| i teraz narysuj sobie wykresy lewej i prawej strony w jednym układzie osi xOy , to zobaczysz kiedy zachodzi ta nierówność |x−1|<|x+1| , która jest równoważna danej , a jak chcesz dalej, to np. |x−1|<|x+1| /² ⇔ (x−1)²<(x+1)² ⇔ x²−2x+1<x²+2x+1 ⇔ −4x<0 /:(−4) ⇔ ⇔ x>0 ⇔ x∊(0;+∞) − szukany zbiór rozwiązań danej nierówności . ...

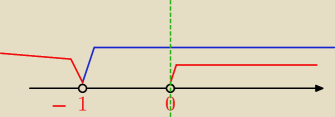
Aga1.: Część wspólna (0,∞)

bezendu1990: @Aga1 dzięki wielkie a co do tego pana to i się wydaję że dobrze tłumaczy a to nie jest miejsce do kłotni kto lepeij tłumaczy. Każdy ma swoje sposoby i każdy jest dobry

bezendu1990: @pigor powiedz po co tyle założeń mam pisać ?