funkcja ;D:

	1
Dziedziną funkcji f(x)=		jest zbiór <2,5>.
	x√3

Prawdziwe jest zdanie: A. Funkcja przyjmuje tylko wartości niewymierne. B. f(2)<f(3) C. Funkcja nie przyjmuje wartości 1. D. Funkcja jest rosnąca.

konrad: A

;D: czemu?

Ajtek: Ponieważ √3 jest l. niewymierną i √3<2

;D: a w odp C, funkcja przyjmuje wartości 1?

konrad: podstaw za x 1 i co Ci wyjdzie?

konrad: a nie sorry, co ja gadam

konrad:

	1
żeby to było równe 1 to x musiałby być równy
	√3

;D:

	1
no właśnie, a		nie należy do dziedziny.
	√3

konrad: no i dlatego C odpada

;D: Jak to? Skoro prawdą jest, że Funkcja nie przyjmuje wartości 1, bo x musiałby być równy

	1
		, a to nie należy do dziedziny.
	√3

;D:

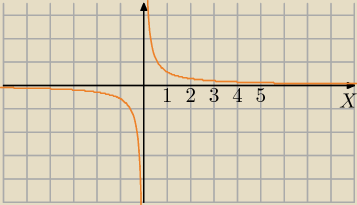
Krzysiek : D odpada bo funkcja jest malejaca na tym zbiorze (wykresem tej funkcji tak w ogole jest hiperbola )

	1
C −odpada bo dla y=1 x rownalby sie x=		a nie nalezy do dziedziny
	√3

b f(2)>f(3) −odpada

	1		√3
A tak jak napisal Konrad . bo zobacz dla x=2 to y=		⇒y=		Tak samo jak
	2√3		6

sprawdzisz dla x=3 x=4 x=5 to jak bedziesz usuwal niewymiernosci z mianownika to zawszew liczniku bedziesz mial √3 a to jest liczba niewymierna

Mila: a) A zdanie nieprawdziwe− funkcja przyjmuje wartości wymierne i niewymierne b)B i D − zdanie nieprawdziwe, bo funkcja w danym przedziale malejąca c) Sprawdzam:

1
	=1
x√3

x√3=1

	1		√3
x=		=		∉D
	√3		3

C − zdanie prawdziwe

;D:

	4√3
ale jak np za x podstawię		, to w przybliżeniu jest równe 2,3, wiec należy do
	3

	1
dziedziny, to z działania wyjdzie mi		, a to jest wymierna.
	4

Mila: do postu z 16:49 dlatego zdanie A jest nieprawdziwe. Tam jest słowo 'tylko".