oblicz Aga: W ostrosłupie prawidłowym trójkątnym pole ściany bocznej jest 4 razy większe od pola podstawy. Oblicz cos kąta między sąsiednimi ścianami bocznymi.

loitzl9006:

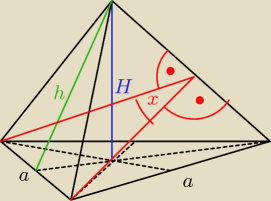
1		a2√3
	a*h=		* 4 = a2√3
2		4

h = 2a√3 Zatem krawędź boczna ma długość

	7
√(a/2)2+(2a√3)2 = √a2/4 + 12a2 =		a
	2

	1		1
zatem pole ściany bocznej to		a*h =		a*2a√3 = √3a2
	2		2

czerwony odcinek (wysokość ściany bocznej opuszczona na krawędź boczną) możesz sobie wyliczyć ze wzoru na pole trójkąta Pole = 1/2 * podstawa(krawędź boczna) * wysokość(czerwony odcinek) i jak obliczysz długość czerwonego odcinka to stosujesz twierdzenie cosinusów w trójkącie równoramiennym z czerwonymi ramionami i podstawie długości a.

Eta:

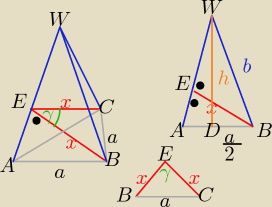
	x2+x2−a2		a2
Z tw. cosinusów w ΔBEC cosγ=		= 1−2
	2x*x		x2

	a*h		a2√3
Z treści zadania: P(ściany ABW)=		= 4*		⇒ h= 2a√3
	2		4

	1		1
dla tej samej ściany:		b*x=		a*h ⇒ bx= a*h
	2		2

	a
z tw. Pitagorasa wΔDBW: b2= (		2+h2
	2

	a2		49		7
b2=		+12a2⇒ b2=		a2 ⇒ b=		a
	4		4		2

	7		4a√3
zatem: bx=ah ⇒		ax= a*2a√3 ⇒ x=
	2		7

	48a2
to x2=
	49

	a2
cosγ= 1−		= ...............dokończ i otrzymasz
	2x2

	47
cosγ =
	96

Eta: Wrrrr