Jak obliczyć dla jakich p i q?
Mei13: Dla jakich p i q liczba 5 jest dwukrotnym pierwiastkiem wielomianu W(x) = x3 − 12x2 + px + q
?
19 paź 20:12
aniab: p=45 q=−50
19 paź 20:24
Mei13: hehe jakbys mogła obliczenia wysłać

19 paź 20:25
aniab: umiesz hornera?
19 paź 20:26
Mei13: umiem

19 paź 20:29
ICSP: Tylko nie Horner

19 paź 20:29
MQ: Skoro jest dwukrotnym pierwiastkiem, to W(x) musi się dzielić bez reszty przez (x−5)
oraz (x−5)2=(x2−10x+25)
Powinny z tego wyjść warunki na p i q.
19 paź 20:33
ICSP: a nie łatwiej wymnożyć :
(x−5)2(x−2) i porównać współczynniki ?
19 paź 20:35
aniab:
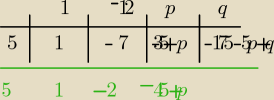
−175 −5p +q = 0
−45+p=0
19 paź 20:35
aniab: ale trzeba wyczuć że trzeci to 2 ;>
19 paź 20:36
ICSP: nie trzeba. Widać od razu.
19 paź 20:37
aniab: zależy kto patrzy ;>
19 paź 20:37
ICSP: każdy uczeń na rozszerzeniu powinien to zobaczyć

19 paź 20:39
MQ: Ad.
ICSP @20:35
Ale trzeba wiedzieć skąd się wzięło (x−2).
Ale przyznaję −− podany przez ciebie sposób bardziej elegancki −− i najprostszy.

19 paź 20:43
pigor: ... lub tak : z warunków zadania :
x3−12x2+px+q= (x−5)
2(x−r)= (x
2−10x+25)(x−r)=
x3−(r+10)x2+(10r+25)x−25r ⇔
⇔ r+10=12 i p=10r+25 i q=−25r ⇔ r=2 i p=20+25 i q=−25*2 ⇒
p=45, q=−50 ..

−−−−−−−−−−−−−−−−−−−−−−−−−−
a propos Hornera, był niezastąpiony, ale ileś lat wstecz w metodach numerycznych, a
nie w takich prostych ...

rachunkach na liczbach całkowitych .
19 paź 20:45
Mila: MQ, Twój sposób, też dobry i prosty.
Podzielić przez (x
2−10x+25)
wynik dzielenia (x−2) i r(x)=x(−45+p)+(50+q)
stąd dla r(x)=0 mamy p i q jak wyżej.
Dla wszystkich panów

19 paź 21:05



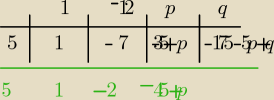 −175 −5p +q = 0
−45+p=0
−175 −5p +q = 0
−45+p=0


 −−−−−−−−−−−−−−−−−−−−−−−−−−
a propos Hornera, był niezastąpiony, ale ileś lat wstecz w metodach numerycznych, a
nie w takich prostych ...
−−−−−−−−−−−−−−−−−−−−−−−−−−
a propos Hornera, był niezastąpiony, ale ileś lat wstecz w metodach numerycznych, a
nie w takich prostych ...  rachunkach na liczbach całkowitych .
rachunkach na liczbach całkowitych .
