nierówność trygonometryczna ada: cos(2x− π/5)≥ 1/2

Ajtek:

1		π
	=cos
2		3

	π		π
cos(2x−		)≥cos
	5		3

	π		π
2x−		≥
	5		3

Dalej sobie poradzisz .

ICSP: Ajtku coś mi się tutaj nie podoba

Ajtek: Cześć ICSP, co skopałem?

ICSP: Witaj Ajtku

	π
Po prostu wydaje mi sie że funkcja cosx w przedziale (0;		) jest malejąca
	2

Mila: Witaj, Ajtek i ICSP. ICSP jak leci na studiach?

Ajtek: No jest. Tylko do czego dążysz mów otwarcie. Ja dzisiaj nie mam specjalnie dnia do matmy .

Ajtek: Hej Mila .

Godzio: Ajtek narysuj sobie cos(2x − π/5) (szkic, nie musisz dokładnie ) narysuj prostą y =

	1
		i sprawdź czy to co podałeś to na pewno prawda
	2

ICSP: Do tego że wedłóg mnie powinno być

	π		π		π
2x − U{π}{5] ≤		oraz 2x −		≥ −
	3		5		3

ale tylko mi się tak zdaje. Lepiej niech to ktoś potwierdzi

ICSP: Witaj Mila Na studiach nudy Wstajesz rano − idziesz na wykłady − zastanawiasz się po co tu jesteś bo i tak nic nie rozumiesz − idziesz na ćwiczenia − wracasz do domu − idziesz spać i tak w kółko

Ajtek: Cholera faktycznie Cześć Godzio. Jak pisałem wcześniej, nie myślę dzisiaj .

ICSP: i okresu nie dodałem

Ajtek: Nie dodałeś okresu, a ja strzeliłem gafę "że łorety"

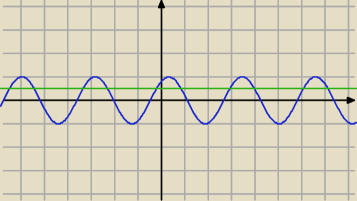
Godzio: Cześć Ja proponuję takie rozwiązanie: Rozwiązujemy równanie:

	π		1
cos(2x −		) =
	5		2

	π		π		π		π
2x −		=		+ 2kπ lub 2x −		= −		+ 2kπ
	5		3		5		3

	4		2
x =		π + kπ lub x = −		π + kπ
	15		15

W ten sposób otrzymaliśmy punkty przecięcia, jeśli sobie narysujemy szkic, to z łatwością możemy odczytać rozwiązanie:

	2		4
x ∊ <−		π + kπ,		π + kπ>
	15		15

Godzio:

	1
Tam powinno być oczywiście −		π
	15

ada: dobrze zrobiłam dzięki