Prośba o kilka przykładów. Sławek: Witam! Mam prośbę o kilka przykładów. Czy mógłby mi ktoś napisać kilka przykładów z nierówności na metodę "wężyka"? Chciałbym sobie poćwiczyć i porozwiązywać jeszcze kilka przykładów a następnie poprosić Was o sprawdzenie moich wyników. Niestety ze strony juz wszystkie przykłady zrobiłem. Pozdrawiam!

Artur_z_miasta_Neptuna: metoda 'wężyka' w sensie szkic wielomianu wysokiego stopnia (x−3)(x−√3)⁴(x+√27)(x²−8)¹⁵(x³+27)³(25−x⁴) > 0 może takie coś na początek

Sławek: o to chodzi zrobie to ale chcialbym wiecej a moze nie az tak skomplikowanych

Krzysiek: 'na początek' ciekawe co będzie na końcu...

Sławek: Jeszcze mam takie pytanko: na stronie pisze, ze rysujemy wężyka od góry jezeli wielomian zaczyna sie liczba dodatnia a od dołu jezeli liczbą ujemną. Nas uczono w szkole jednak, że zależy to od znaku najwyższej potęgi. To jak to wkoncu jest naprawde?

Artur_z_miasta_Neptuna: współczynnik 'a' to nic innego jak 'znak przy najwyższej potędze' ponieważ w ogólnym zapisie masz: W(x) = a*xⁿ + b* xⁿ⁻¹ + ......

Artur_z_miasta_Neptuna: inaczej ... znak współczynnika 'a' oraz znak przy najwyższej potędze to jest to samo

Sławek: a i jeszcze taka rzecz: Jak mam x(x−3)(−x+2) no to wszystkie potęgi tu są równe a znak pierwszy + wiec zaczne rysowac od dołu czy od góry?

Artur_z_miasta_Neptuna: ojjj widać nie rozumiesz o co chodzi. jakbyś wymnożył nawiasy to byś dostał postać W(x) = ax³ + bx² + cx + d a jak zobaczyć znak 'a' bez wymnażania bardzo latwo: patrzysz na znaki najwyższej potęgi 'x' W KAŻDYM nawiasie i jest mnożysz ze sobą +1 * +1 * (−1) = −1 ... czyli a<0

Aga1.: Od dołu, bo wymnażasz wszystkie współczynniki sprzed x. 1*1*(−1)=−1

Artur_z_miasta_Neptuna: ale gdyby było: x(x−3)(−x+2)² to by było +1 * +1 * (−1)² = +1 ... czyli a>0

Artur_z_miasta_Neptuna: rozumiesz teraz jak wyglada 'procedura'

Sławek: tak właśnie robiłem ale myslalem, ze kryje sie za tym jakis inny sposob niz wymnazanie all. Prosze w takim razie o wiecej przykładów, niekoniecznie tak trudnych jak ten wyżej

Artur_z_miasta_Neptuna: ale tamten nie jest trudny zrobisz ten to juz każdy zrobisz

Sławek: i tak chce wiecej, chce miec pewnosc

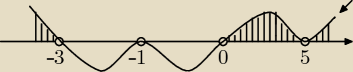
Heniek: 2x³(x − 5)²⁸(x + 1)³²(x + 3) > 0

Sławek: ale nie rysuj mi, daj mi sie samemu wykazać

Sławek: dobra, wymiękam Przykład neptuna za trudny bo niewiem co zrobic z (x² − 8) oraz z (25−x⁴) oraz z (x³ + 27) no bo x² − 8 = (x−√8)(x+√8) no ale to jest do p¹⁵ i jak to rozpatrzec?

ICSP: (x² − 8)¹⁵ = (x−√8)¹⁵(x + √8)¹⁵

Sławek: aaaa aaa 25−x⁴? albo x³ + 27 ? to ost to bedzie (x³ + 3³ ) ale niewiem jak to wykorzystac.

ICSP: 25 − x⁴ = −(x⁴ − 25) = −(x² + 5)(x−√5)(x+√5) x³ + 3³ = (x+3)(x² − 3x + 9)

Sławek: aha to z 27 to wiem, rozwale wzorem ale z tym 25 niewiem co

Sławek: aha w ten sposób. Dobra próbuję robić

Sławek: ale ta funkcja kwadratowa nie ma miejsc zerowych, to co z nia?

ICSP: pomyśl jaka jest jej wartość dla każdego x

Sławek: 0?

ICSP: czekaj Δ < 0 czyli nie ma miejsc zerowych a teraz piszesz mi że dla każdego x wartość funkcji jest równa 0 Czyli funkcja posiada nieskończenie wiele miejsc zerowych ?

Sławek: nie napewno nie 0, niewiem.

Sławek: nie no strzelilem odpowiedzia bez zastanowienia

ICSP: to podstaw kilka liczba zamiast x. Policz ile ci wyjdzie i wyciągnij wnioski

Artur_z_miasta_Neptuna: nie 0 tylko >0 x² ≥ 0 x² + 5 ≥ 5 > 0 (brak miejsc zerowych)

Sławek: no ze wartosc zawsze bedzie −

Artur_z_miasta_Neptuna: a specjalnie w przykładzie dalem 'różne' rzeczy byś przećwiczył WSZYSTKO (rozkład ze wzorów skróconego mnożenia ... zauwazenie, że tutaj brak miejsc zerowych ... 'odbijanie' przy parzystych potęgach ... a co robi się przy wysokich potęgach nieparzystych ... itd.)

Sławek: no wlasnie ja zauwazylem, ze tu nie ma miejsc zerowych i niewiem co z tym fantem teraz zrobic, o to chodzi wlasnie

Sławek: dobra wyszło mi: (−∞,−8)u(−√27,−3)u(−√5,√3)u(√3,√5)u(3,8)

Sławek: prosze o sprawdzenie

Sławek: i jak?

Sławek: czemu nikt tego nie chce sprawdzic?

Aga1.: −8 nigdzie nie ma.

Sławek: tam jest zamiast 8 i − 8 √8 i −{8} pomyliło mi się a tak poza tym?

ICSP: to poraw √8 < 3 przecież

Sławek: aha no tak, dobra pewnie takich błędów mam tysiace w tym przykładzie. Zdecydowanie too hard. nie ma sensu robic az tak trudnych bo i tak sie gdzies pomyle. Wazne ze na stronie all zrobilem i mi dobrze poszło