wyznacz dziedzine ania :

	x−5
bardzo prosze m,i wytlumaczyc o co chdozi i jak to zrobic. wyznacz dziezdine 2x2−
	x−2

co oznacza x₂ ? prosze niech ktos ze mna zrobi ten przyklad

ania : prosze mi wytlumaczc jak to sie robi

ania : jak ktos zyczliwy zrobi ze mna 1 przyklad to inne zrobie sama na podstawie tego blagam pomozcie chce sie czegos nauczyc a nie spisac od kogos w szkole

Artur_z_miasta_Neptuna: na pewno dobrze napisalaś przykład

Artur_z_miasta_Neptuna: bo szczerze mowiąc to nie ma NAJMNIEJSZEGO sensu

ania :

	x−5
tak 2x2 −
	x−2

ania :

	x+1
i polecenie to wyznacz dziezdine wyrażenia 3 dostalismy do zrobienia drugi to		:
	x−3

	x+5
	x−4

ania :

	1		1
a trzeci to x−		+ √x−3−
	x+4		x

ania : mialam nadzieje ze mi ktoś tutaj pomoze bo sama nie umiem zrobic tego nie rozumiem w ogole tego wyznaczania dziedziny wyrazenia

Artur_z_miasta_Neptuna: to w pierwszym może jednak x² powinno być w drugim:

x+1   x−3
x+5   x−4

co musi być spełnione, aby należeć do dziedziny 1) mianownik górnego ułamka ≠0 czyli x−3 ≠0 2) mianownik dolnego ulamka ≠0 czyli x−4 ≠0

	x+5
3) mianownik 'głównego' ułamka ≠0 czyli		≠ 0
	x−4

i na podstawie tego wyznaczasz dziedzinę w trzecim 1) mianownik ułamka ≠0 2) liczba pod pierwiastkiem kwadratowym (a tak naprawdę PARZYSTEGO stopnia) ≥0 3) mianownik drugiego ułamka ≠0

Artur_z_miasta_Neptuna: a dlaczego takie są warunki?

	1
a powiedz mi ile to jest		no wlaśnie ... nie wiesz ... ja tez nie wiem nikt
	0

tego nie wie albo ile to jest √−5 no właśnie ... też nie wiesz ... na poziomie gimnazjum/liceum nikt tego nie wie (a reszta cicho siedzieć ) i stąd te warunki

ania :

	x−5
no nie wiem czzemu jest x2 moze to blad w druku zrobmy 2x2 −		czyli zaczynam od
	x−2

mianownika x−2 nie moze rownac sie zero tak?

ania : haha czyli reszta wie

Artur_z_miasta_Neptuna: tak dokładnie od tego zaczynasz ... i tylko to tutaj masz no to gratuluję ... przećwicz to sobie jeszcze

ania : i to w założeniach napiasć zał. x−2≠0 x=2 i co dalej mam zrobic

Artur_z_miasta_Neptuna: x≠2 czyli D_f = R / {2}. koniec zadania

Aga1.: x≠2 tak zostawić lub zapisać w formie równoważnej D=R−{2} lub D=(−∞,2)U(2,∞)

ania : ok cyzli jesli napisze po prostu Df=R/{2} to tak już moze to zostac i tak moge wpisac w odpowiedz?

ania : ja myslala ze trzeba bedzie cos liczyć tutaj,, a czy osi nie powinno się narysowac do tego i to zaznaczyc?

ania :

	x+5
to podpunkcie b bedzie x−3≠0 x≠3 x−4≠0 x≠4 i		≠0 − i to juz tak zostawiam ?
	x−4

ania : czy napisac x≠−5 i x≠4

Artur_z_miasta_Neptuna:

x+5
	≠ 0 // *(x−4) bo x−4 ≠0 (patrz poprzedni warunek)
x−4

czyli x+5 ≠ 0 czyli x≠ −5

a
	≠ 0 .... wtedy ZAWSZE a≠0 (oraz dodatkowo wcześniej założenie, że b≠0)
b

ania : czyli Df= R/{3,4−5} ?

ania : a podpunkcie trzecim x+4≠0 x≠−4 √x−3≥0 i x≠0 ?

Aga1.: tak.

ania : a jak zapisac w podpunkcie 3 Df=R/{−4,i dale jak wpisac ten pierwiastek i x

Aga1.: w trzecim x≠−4 i x−3≥0 i x≠0

ania : ale jak to zapisac w odpowiedzie Df= R/{?}

Aga1.:

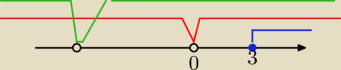
Aga1.: Wyznacz część wspólną trzech warunków.

ania: oka w porpzednich dwoch przykladach nie rysujemy osi>?

Aga1.: Nie było takiej potrzeby, ale jak się uprzesz, to możesz podawać odpowiedź jako sumę kilku przedziałów.

ania: to bedzie D=(−∞,3)U<3,∞)w smie czemu tylklo 3 jest jak tam est jeszcze x nie moze rownac sie −4

ania: ? cy moze mi ktos jeszcze raz ostatni przyklad wytlumaczyc

Aga1.: Część wspólna , to tam, gdzie występują trzy kolory, a −4 wyrzuciłam zaznaczając kółeczkiem pustym (pierwszy z lewej strony)

ania: trzy kolory to bd D= <3,+∞) ?

Aga1.:

	1		1
x−		+√x−3−
	x+4		x

x+4≠0, x≠−4, czyli x∊(−∞,−4)U(−4,∞) i x≠0 , czyli .... i x−3≥0, x≥3, czyli x∊<3,∞) Przedziały zaznaczyłam na osi liczbowej, a część wspólna , to dziedzina D=<3,∞)

Aga1.: Tak Aniu.

ania : a w podpunckie 1 D=(−∞,2)U(2,∞) cze przy 2 jest nawias ) a nie > cemu to przedzial otwarty a nie zamkniety nie powinno byc x∊<2,+∞) wiec D=(−∞,2> U <2+∞) ?

Aga1.: Przecież 2 nie należy do dziedziny, więc nie może być przedział domknięty. <a,b) przedział lewostronnie domknięty ( a należy do przedziału, prawostronnnie otwarty, b nie należy do przedziału

ania : acha ale powiedz mi prosze bo mnnie to zaciekawilo jak bysmy chcialy narysowac do podpunktu 1 i 2 wykres os z przedialami to akby to wygladalo ?

Aga1.: Np. z godz.16;05 D=R−{−5,3,4} D=(−∞,−5)U(−5,3)U(3,4)U(4,∞)