Granice funkcji
bartek: Witam
Proszę o pomoc oraz ewentualne sprawdzenie poniższych granic funkcji:
| | arcctg4x | |
1) lim przy x−>0 |
| nie potrafię przekształcic tego arc ctg
|
| | 3x | |
| | sin2x | |
2) lim przy x−>0 |
| nie wiem co zrobic z sin2, próbowałem rozpisac jako sinsin, ale |
| | x | |
nie za wiele to dało
| | ln(1+√x) | |
3) lim przy x−>0 |
|
|
| | 3√x | |
4) lim przy x−>0 sin3xctg5x kolejny raz nie wiem co zrobic z ctg
| | tgx−sinx | |
5) lim przy x−>0 |
| nieszczęsny sin3
|
| | sin3x | |
| | sin2x−sin4x | | 2x(sin−sin2) | |
6) lim przy x−>0 |
| = |
| =2 można w ten sposób?
|
| | sinx−sin2x | | x(sin−sin2 | |
| | arctg(3x−9) | |
7) lim przy x−>3 |
|
|
| | x2−9 | |
Proszę o w miarę rozpisanie przykładów.
Pozdrawiam

18 paź 22:41
bartekS:
18 paź 22:54
bartekS: Ma ktoś jakiś pomysł?
18 paź 23:42
Beti: Mam pomysła na kilka przykładów, ale bez gwarancji, że to jest dobrze

| | sin2x | | sinx*sinx | | sinx | |
2) lim |
| = lim |
| = limsinx*lim |
| = 0*1 = 0 |
| | x | | x | | x | |
| | cos5x | | sin3x | | cos5x | |
4) limsin3xctg5x = limsin3x* |
| = lim |
| * |
| = |
| | sin5x | | | | | |
18 paź 23:50
pigor: ... np. tak :
| | arctg4x | | 4x | | arctg4x | | 4 | | 4 | |
1) limx→0 |
| = limx→0 |
| * |
| = |
| * 1= |
| ; |
| | 3x | | 3x | | 4x | | 3 | | 3 | |
−−−−−−−−−−−−−−−−−−−−−−−
| | sin2x | | sinx | |
2) limx→0 |
| = limx→0 x* ( |
| )2 = 0*12= 0 ; |
| | x | | x | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−
| | ln(1+√x) | | √x | | ln(1+√x) | |
3) limx→0 |
| = limx→0 |
| * |
| = |
| | 3√x | | 3√x | | √x | |
| | ln(1+√x) | |
= limx→0 6√x * |
| = 0*1= 0 ; |
| | √x | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
| | sin3x*cos5x | |
4) limx→0 sin3xctg5x= lim{x→0} |
| = |
| | sin5x | |
| | 3x | | sin3x | | 5x | | 3 | | 3 | |
= limx→0 |
| * |
| * |
| * cos5x= |
| *1*1*1= |
| ; |
| | 5x | | 3x | | sin5x | | 5 | | 5 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
| | tgx−sinx | | sinx−cosx*sinx | |
5) limx→0 |
| = limx→0 |
| = |
| | sin3x | | cosx*sinxsin2x | |
| | sinx(1−cosx) | | 1−cosx | |
= limx→0 |
| =limx→0 |
| = |
| | cosx*sinx(1−cos2x) | | cosx(1−cosx)(1+cosx) | |
| | 1 | | 1 | | 1 | |
= limx→0 |
| = |
| = |
| ; |
| | cosx(1+cosx) | | 1(1+1) | | 2 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
| | sin2x−sin4x | | sin2x−2sin2xcos2x | |
6) limx→0 |
| = limx→0 |
| = |
| | sinx−sin2x | | sinx−2sinxcosx | |
| | sin2x(1−2cos2x) | | 2sinxcosx(1−2cos2x) | |
=limx→0 |
| =limx→0 |
| = |
| | sinx(1−2cos) | | sinx(1−2cosx) | |
| | 2cosx(1−2cos2x) | | 2*1(1−2*1) | |
= limx→0 |
| = |
| = 2*1= 2 ; |
| | (1−2cosx) | | (1−2*1) | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
| | arctg(3x−9) | | arctg3(x−3) | |
7) limx→3 |
| = limx→3 3* |
| = |
| | x2−9 | | 3(x−3)(x+3) | |
| | 3 | | arctg3(x−3) | | 3 | | 3 | | 1 | |
= limx→3 |
| * |
| = |
| * 1= |
| = |
| ... i tyle . ...  |
| | x+3 | | 3(x−3) | | 3+3 | | 6 | | 2 | |
19 paź 00:10
bartekS: Coś niesamowitego

dzięki

. Powiedz jak możesz skąd w 3 jest
6√x.
19 paź 10:54
Aga1.: | √x | | 6√x3 | | x3 | |
| = |
| =6√ |
| =6√x, gdy x>0 |
| 3√x | | 6√x2 | | x2 | |
19 paź 10:59
bartekS: Czyli to jest po to, aby znaleźc jakby wspólny pierwiastek? Są na to jakieś wzory?
W 1 chodziło mi o arc ctg.

19 paź 11:36
bartekS: Wiem, że to już natręctwo z mojej strony, ale mam jeszcze kilka pytań:
| | 5x | | sin5x | |
W 4 czy |
| to jest to samo co |
| , mam na myśli wzór granicy funkcji dla sin |
| | sin5x | | 5x | |
właśnie, bo jeśli nie to dlaczego to też jest równe 1?
Skąd w 6 ten cos? Mnożymy w ten sposób 2sinx=sin2x czy po prostu 2sinx
19 paź 12:21
pigor: ... otóż,
w 4) no tak, to samo, choć ...

nie takie samo, bo
| | 5x | | 1 | | 1 | |
limx→0 |
| = limx→0 |
| = |
| = 1 ; |
| | sin5x | | | | 1 | |
w 6) bo jest wzór (np. w tablicach który "musisz" znać) , że można zamienić
sin2x= 2sinx*cosx, a podobnie przydaje się np. wzór
cos2α=cos2α−sin2α. ...

19 paź 13:06
Mila: pigor

W pierwszym jest arcctg(4x) czy arctg(4x) ? bo wyszło mi
∞.
19 paź 13:49
pigor: ... no tak, ja liczyłem jako arctg4x (arkus tangens) a tam faktycznie jest cotangens,
przepraszam .

19 paź 13:53
johny11: Ok, teraz już rozumiem co jednak z arc ctg, zapisac to jako cos przez sin?
19 paź 14:49
pigor: ... może tam miało być arctg4x

ale jak nie, to ja bym robił wtedy np. tak :
| | arcctg4x | | cost | |
limx→0 |
| = | arcctg4x=t ⇒ ctgt=4x ⇒ x=14ctgt= |
| i x→0 ⇒ |
| | 3x | | 4sint | |
| | π | | π | | t | |
⇒ ctgt→0 ⇒ t→ |
| | = lim t→ |
| |
| = |
| | 2 | | 2 | | | |
| | π | | 4sint | | 4*1 | | 4 | |
= lim t→ |
| |
| = |
| = [ |
| ]= ∞ . ...  |
| | 2 | | 3cost | | 3*0 | | 0 | |
19 paź 15:26
bartekS: Czyli jak się wprowadza zmienną pomocniczą to można pominąc arc?
19 paź 15:56
pigor: ... , ja
nic nie pomijam, tylko zgodnie z definicją arcusa funkcji f (czyli z funkcji
odwrotnej do f)
przechodzę (wracam) na funkcję f i tyle . ...

19 paź 16:14
bartekS: Masz rację dzięki

19 paź 17:00
bartekS: Jak policzyc coś takiego:
| | √x+9−3 | |
lim przy x−>0+ |
| ? |
| | x | |
19 paź 18:48
aniab: pomnożyć górę i dół przez √x+9+3
19 paź 18:52
bartekS: Zapytam się jeszcze, jak to jest z opuszczaniem wartości bezwzględnej:
1)|x+4| kiedy, x−>−4− oraz kiedy x−>−4+
2)|x−4| kiedy, x−>−4− oraz kiedy x−>−4+
19 paź 20:25
bartekS: Ma ktoś jakieś propozyzje?
19 paź 22:26
bartekS: Może jednak ktoś podpowie, przyda mi się to na przyszłość, czyli kolokwium

20 paź 21:43
Mila:
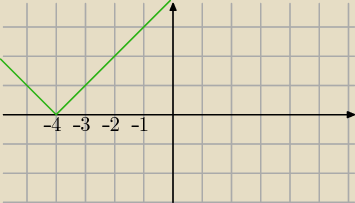
|x+4|=x+4 dla x→−4
+
|x+4|=−x−4 dla x→−4
−
20 paź 22:08
bartekS: W takim razie:
| | x | | x | |
1) lim przy x−>−4− |
| = |
| =−∞
|
| | |x+4| | | −x−4 | |
| | x | | x | |
2) lim przy x−>−4+ |
| = |
| =+∞  |
| | |x+4| | | x+4 | |
20 paź 22:38
Mila: druga granica też ( −
∞)
| | −3,999 | |
[ja robię podstawienie |
| →−∞] |
| | −3,999+4 | |
20 paź 22:46
bartekS: | | A | |
Z podstawowego wzoru [ |
| ]=+ lub −∞, gdzie A to stała
|
| | 0 | |
| | −4 | |
Czyli jak |
| to powinno chyba byc +∞  |
| | 0+ | |
20 paź 23:01
Mila: Ujemna : dodatnia=ujemna
(−4):0,000000000000000001=−4*1018<0
20 paź 23:07
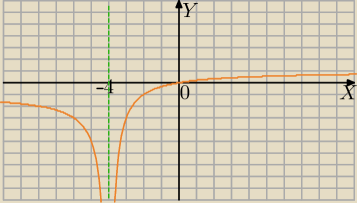
Mila:
20 paź 23:09
bartekS: Czyli ''stała'' też ma wpływ na wynik, w zależności oczywiście od mianownika

Np 1)dla licznika − mianownika + całośc bedzie −

2) dla licznika − mianownika − całośc +

3) dla licznka + mianownika − całośc −

20 paź 23:14
Mila: Tak, normalnie znaki jak przy iloczynie, czy też ilorazie.
20 paź 23:21



 dzięki
dzięki  . Powiedz jak możesz skąd w 3 jest 6√x.
. Powiedz jak możesz skąd w 3 jest 6√x.

 nie takie samo, bo
nie takie samo, bo

 W pierwszym jest arcctg(4x) czy arctg(4x) ? bo wyszło mi ∞.
W pierwszym jest arcctg(4x) czy arctg(4x) ? bo wyszło mi ∞.

 ale jak nie, to ja bym robił wtedy np. tak :
ale jak nie, to ja bym robił wtedy np. tak :




 |x+4|=x+4 dla x→−4+
|x+4|=−x−4 dla x→−4−
|x+4|=x+4 dla x→−4+
|x+4|=−x−4 dla x→−4−



 Np 1)dla licznika − mianownika + całośc bedzie −
Np 1)dla licznika − mianownika + całośc bedzie − 2) dla licznika − mianownika − całośc +
2) dla licznika − mianownika − całośc + 3) dla licznka + mianownika − całośc −
3) dla licznka + mianownika − całośc −