wykresy zadanie: Proszę o pomoc przy zadaniu, w ogole nie wiem jak sie za nie zabrac zad. naszkicuj wykres i odczytaj miejsca zerowe funkcji dla x∊<−2π, 2π> a) y=cos(x+π\2) b) y= −sin(x+π\2) c) y= tg(x)−1 d) y= ctg (x+ 3π\2)

ewa:

	π
a) narysuj wykres y=cosx i przesuń go w lewo wzdłuż osi x o
	2

	π
, czyli o wektor [−		,0]
	2

ewa:

	π
b) narysuj wykres y=sinx, przesuń go o		w lewo wzdłuż osi x, czyli o wektor
	2

	π
[−		,0], a następnie tak otrzymany wykres odbij symetrycznie względem osi x
	2

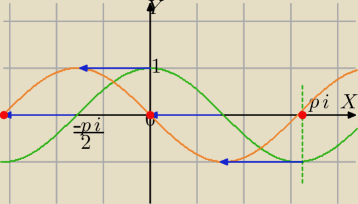Mila: 1) a) rysujesz wykres y=cosx

	−π
b) przesuwasz = wektor [		,0]
	2

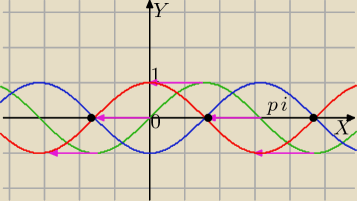Mila: 1) y=sinx

	−π
2) przesunięcie o wektor [		;0] czerwony wykres
	2

3) odbicie symetryczne względem osi OX niebieski wykres Zaznaczyłam miejsca zerowe Musisz narysować te funkcje w przedziale <−2π;2π>

zadanie: Dziękuję Wam bardzo za odpowiedzi Dobranoc

Mila:

Mila: c) y= tg(x)−1 1) rysujesz wykres tgx 2) przesuwasz o wektor [0;−1] jedna jednostka w dół.

	3π
d) ctg (x+		)
	2

1) rysujesz wykres funkcji y=ctgx

	3π
2) Przesuwasz w lewo o wektor [−		;0]
	2