Równania kwadratowe. moth: Bartek−chodziarz, na długich dystansach chodzi z śr szybkością 2 km/h, a Kuba−biegacz z szybkością 8 km/h. Treningi rozpoczynają z tego samego miejsca, każdy po innej z dwóch prostopadłych do siebie ścieżek. Bartek rozpoczyna trening o godzinę wcześniej niż Kuba. a.) Po jakim czasie od momentu startu Kuby odległość między nimi będzie równa 50 km/h? b.) Ile km przejdzie w tym czasie Bartek? Z twierdzenia Pitagorasa?

Maslanek: Ja bym to zrobił po fizycznemu x(t)=2t y(t)=8t Z warunkami zadania: x(t)=2t y(t−1)=8(t−1)=8t−8 d(t)=√x(t)²+y(t)² a) d(t)=50 b) x(d(t)=50)=2*t_d(t)=50

johnny : ,,odległość między nimi będzie równa 50 km/h?,, odległość w km/h ? o.O

moth: Jak po fizycznemu to ja odpadam Poproszę o tłumaczenie Rozwiązanie mam: a.) Po 6 h b.) 14 km. Tylko sposób...?

moth: Głupoty piszę, mój błąd... 50 km, bez h..

johnny : z exela: godz b k odleglosc 1 2 0 2 2 4 8 8,94427191 3 6 16 17,08800749 4 8 24 25,29822128 5 10 32 33,52610923 6 12 40 41,76122604 7 14 48 50 8 16 56 58,24087911 9 18 64 66,48308055 10 20 72 74,72616677 zalezność a² + b² = c² to c= √a²+b² a to droga bartka b to droga kuby c to odległość miedzy nimi

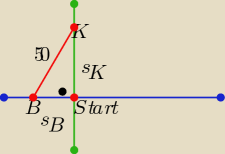
Eta: t −−−czas od momentu startu Bartka , t>0 t−1 −−− czas startu Kuby s_K −−− droga przebyta przez Kubę s_B −− droga przebyta przez Bartka s= V*t ⇒ s_K= 8*(t−1) , s_B= 2*t z tw. Pitagorasa: (2t)²+ [8(t−1)]²= 50² otrzymasz równanie kwadratowe : 17t²−32t−609=0 Δ= 42436, √Δ=206 t= 7 h 1/ po czasie t−1= 6h (od momentu startu Kuby) 2/ bartek przejdzie wtym czasie drogę S+B= 2*t=2*7= 14 km

Eta: poprawiam zapis: 2/ Bartek przejdzie w tym czasie drogę S_B = 2*t= 2*7= 14 km