Jak się do tego zabrać?
Kaśka:
18 paź 19:45
Kaśka: Tam w ułamku jest 5x
18 paź 19:46
Maslanek: Mnożysz przez (2−5
x)
2 i dalej do przodu

I wyznaczasz 2−5
x≠0.
18 paź 19:48
Piotr:
nie lepiej 5x = t ?
18 paź 19:54
Maslanek: W końcu i tak to musi zrobić...
18 paź 19:55
Kaśka: a nie moze ktos tego zrobic bo ja jestem po podstawie a to jest takie troch rozszerzenie? (na
marginesie − zadanko z materialu do kolosa na polibudzie

)
18 paź 19:56
18 paź 19:58
Maslanek: 2−5
x≠0
5
x≠2
x≠log
52
Teraz równanie (t=5
x; t>0):
t(t−2)
2+15(2−t)<0
t
3−2t
2+4t+30−15t<0
t
3−2t
2−11t+30<0
Dalej rozwiązuj sama

18 paź 19:59
Mila:
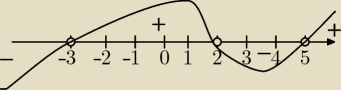
II sposób
5
x=t i t>0
| | 15 | |
t+ |
| <0 sprowadzamy do wspólnego mianownika |
| | 2−t | |
| t(2−t)+15 | | 2t−t2+15 | |
| <0 ⇔ |
| <0 mnożę licznik i mianownik przez (−1) |
| 2−t | | 2−t | |
U{t
2−2t−15}{{t−2}<0
Δ=64
t
1=−3 lub t
2=5
t∊(2;5)⇔
5
x>2 i 5
x<5⇔x>log
52 i x<1
19 paź 13:23
pigor: ... no to jeszcze może łopatologicznie rzecz ujmując z własności
potęgi i funkcji wykładniczej dane równanie jest równoważne kolejno np. :
| | 15 | | 15 | |
5x+ |
| <0 ⇔ 5x− |
| <0 /* (5x−2)>0lub(5x−2)<0 ⇔ |
| | 2−5x | | 5x−2 | |
⇔ (5
x(5
x−2)−15<0 i 5
x−2>0)
lub (5
x(5
x−2)−15>0 i 5
x−2<0) ⇔
⇔ (5
2x−2*5
x+1<16 i 5
x>2)
lub (5
2x−2*5
x+1>16 i 0<5
x<2) ⇔
⇔ [(5
x−1)
2<4
2 i 5
x>2]
lub [(5
x−1)
2>4
2 i 0<5
x<2] ⇔
⇔ (5
x−1<4 i 5
x>2)
lub (|5
x−1|>4 i 0<5
x<2) ⇔
⇔ 2< 5
x <5
lub [(5
x−1<−4 lub 5
x−1>4) i 0<5
x<2] ⇔
⇔ lg
52< lg
55
x <lg
55
lub (5
x<−3 i 0<5
x<2)
lub (5
x>5 i 0<5
x<2) ⇔
| | lg2 | |
⇔ lg52< xlg55 <1lub x∊∅lubx∊∅ ⇔lg52< x<1⇔ |
| <x<1 ⇔ |
| | lg5 | |
⇔
x ∊ (lg52 ; 1) − szukany
zbiór rozwiązań danej nierówności ...

19 paź 14:59
pigor: ... rozwiązanie powyżej oczywiście dla tych, co ...

na morzu, czyli rozszerzeniu i może nie
lubią zmiennej pomocniczej (jak np. ja), ale za to ...

lubią podstawowe prawa logiki i
teorii mnogości (zbiorów i działań na nich) . ...

no i lubią porządek w zapisie i np.
układzie emotikonek

19 paź 15:06
 I wyznaczasz 2−5x≠0.
I wyznaczasz 2−5x≠0.
 )
)
 http://www.wolframalpha.com/input/?i=5%5Ex+%2B+15%2F%282-5%5Ex%29%3C0
http://www.wolframalpha.com/input/?i=5%5Ex+%2B+15%2F%282-5%5Ex%29%3C0

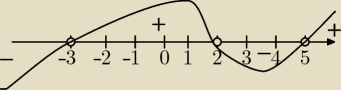 II sposób
5x=t i t>0
II sposób
5x=t i t>0

 na morzu, czyli rozszerzeniu i może nie
lubią zmiennej pomocniczej (jak np. ja), ale za to ...
na morzu, czyli rozszerzeniu i może nie
lubią zmiennej pomocniczej (jak np. ja), ale za to ...  lubią podstawowe prawa logiki i
teorii mnogości (zbiorów i działań na nich) . ...
lubią podstawowe prawa logiki i
teorii mnogości (zbiorów i działań na nich) . ...  no i lubią porządek w zapisie i np.
układzie emotikonek
no i lubią porządek w zapisie i np.
układzie emotikonek 