Jednokładność
Me: Witam średnio rozumiem zadanie.
Oblicz pole figury F', która jest obrazem figury F w jednokładności o środku (0,0) i skali k
F= { (x,y) należy do R2 : x2 + 8x + y2 − 4y − 5 ≤0 i y≤2 } k = 2
17 paź 23:56
Me: Proszę o pomoc wyliczyłem wektor SO' wyszło mi [−8,4] czyli równanie powstałego okręgu to
(x+8)2+(y−4)2=r2 i nie wiem jak obliczyć to pole
18 paź 00:05
kowal:
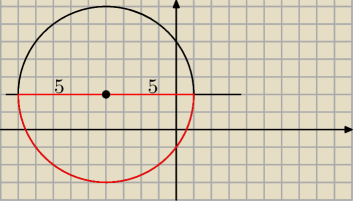
F; (x + 4)
2 + (y − 2)
2 ≤ 5
2
P
F' = P
F*k
2
18 paź 00:11
MQ: 1. Wyznaczasz równanie okręgu pierwotnego:
w postaci (x−x0)2+(y−y0)2=r2
2. Pole figury F' = πr2*k2
18 paź 00:13