Mam takie coś:
jak to ogarnac?: Mam takie coś:
wyszło mi, że x= 0 lub x = 1 lub x = −1, jak to dokonczyc?

17 paź 22:31
Pestek: chyba w odp masz 0,1,−1 a sam nic nie zrobiłes
17 paź 22:32
ICSP: D : x ∊ R\{0}
2x > 3x − x
3
x
3 − x > 0
(x−1)x(x+1) > 0 ⇒ x ∊ (−1;0) suma (1 ; +
∞)
17 paź 22:32
aniab:
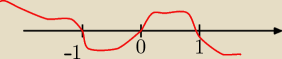
x∊(−1;0)u(1+
∞)
17 paź 22:33
PuRXUTM: | 2 | | 3 | |
| − |
| +x>0/*x2 − bo nie wiemy czy x jest dodatnie czy ujemne bo gdyby było ujemne to |
| x | | x | |
musielibyśmy zmienić zwrot nierówności
2x−3x+x
3>0
x
3−x>0
x(x
2−1)>0 dokończ

17 paź 22:34
jak to ogarnac?: nie nie mam w odpowiedzi poprostu niewiem jak wyznacza sie przedzialy jak sa 3 miejsca zerowe.
ICSP jak do tego doszedles? chodzi mi o ten dół, jak wyznaczyc przedział

17 paź 22:34
17 paź 22:35
aniab: rysuje się wężyk
17 paź 22:35
jak to ogarnac?: PuRXUTM− wiem, ze sie mnozy przez x
2 i wiem

wiem doszedlem do tego co ty i wlasnie nie
umiem narysowac czegos takiego jak aniab

jak to sie robi?

17 paź 22:35
Pestek:
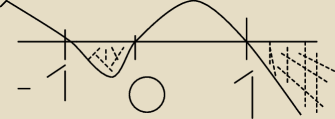
17 paź 22:36
17 paź 22:36
jak to ogarnac?: aha a dlaczego ania wtedy zaczela od dolu a nie od góry? przeciez jest x(x2 − 1 ) a więc
wielomian zaczyna sie od liczby dodatniej, no bo 1x.
17 paź 22:38
ICSP: ania zrobiła sam rysunek. W jej wypadku wielomian wygląda następująco : −x3 + x < 0 co
jest identyczne z moim x3 − x > 0
17 paź 22:39
ICSP: sama*
Przepraszam.
17 paź 22:40
aniab: ja miałam po drugiej stronie
(o 22.32 masz)
2x > 3x − x3
0>x−x3 dlatego od dołu i to co pod spodem
17 paź 22:41
jak to ogarnac?: a jak mam dla tego drugiej czesci wielomianu: x
2−1 wiec x − 1 lub x = −1 prawda? to dla obydwu
tych wynikó się odbic od osi?

17 paź 22:42
aniab: każdy występuje raz więc przechodzi jakbyś miał (x−1)2 to się odbije
17 paź 22:51
jak to ogarnac?: rozumiem, ale teoretycznie moglbym zrobic dla (x−1) (x+1) , prawda?

i wtedy by sie nie
odbijało?

17 paź 22:54
jak to ogarnac?: słuchajcie a mam jeszcze takie cos:
| x+1 | |
| >0 i za chiny niewiem jak z tego wyjsc na miejsca zerowe... |
| −x | |
17 paź 22:54
aniab: pomnożyć obustronnie przez x2
17 paź 22:55
ICSP: | x+1 | |
| > 0 ⇒ x(x+1) < 0 ⇒ x ∊ (−1;0) |
| −x | |
17 paź 22:56
jak to ogarnac?: oraz to:
17 paź 22:56
jak to ogarnac?: ok a to drugie?

to trudniejsze
17 paź 22:56
jak to ogarnac?: hmm?

17 paź 23:12
aniab: na jedna stroną i do wspólnego mianownika .. a potem razy kwadrat mianownika
17 paź 23:13
PuRXUTM: do wspólnego mianownika dziedzina i obustronnie razy mianownik do kwadratu
17 paź 23:13
ICSP: D : x ∊ R\{0;2}
x(x−2) ≤ 0 ⇒ x ∊ (0;2)
17 paź 23:14
17 paź 23:14

 x∊(−1;0)u(1+∞)
x∊(−1;0)u(1+∞)


 wiem doszedlem do tego co ty i wlasnie nie
umiem narysowac czegos takiego jak aniab
wiem doszedlem do tego co ty i wlasnie nie
umiem narysowac czegos takiego jak aniab  jak to sie robi?
jak to sie robi? 

 https://matematykaszkolna.pl/strona/142.html
https://matematykaszkolna.pl/strona/142.html

 i wtedy by sie nie
odbijało?
i wtedy by sie nie
odbijało? 
 to trudniejsze
to trudniejsze
