Oblicz objętość i pole powierzchni całkowitej bryły powstałej z obrotu trójkąta. bryłka: Pomóżcie. Mam problem z narysowaniem figury. Dwa boki trójkąta mają długość 4 cm i 8 cm, a kąt między tymi bokami ma miarę α=120 stopni. Oblicz objętość i pole powierzchni całkowitej bryły powstałej z obrotu trójkąta wokół prostej zawierającej bok o długości 8 cm.

Eta: Powstałą bryłą jest duży stożek ACD z wydrążonym w podstawie małym stożkiem DBC V(br)= V(dużego st. ) −V( małego st.) P_c( bryły )= P_b( dużego st.) + P_b( małego st.)

	1		1
V(br) =		πr2( |OA|−|OB|=		πr2*|AB| , |AB|= 8
	3		3

teraz należy obliczyć długość "r"

	1
P(ΔABC) =		*4*8*sin120o = ......... =8√3
	2

	1
i P(ΔABC)=		*r*8 ⇒ 4r= 8√3 ⇒ r= 2√3
	2

V( br)=.......... dokończ Do wyznaczenia pola powierzchni potrzebne są długości obydwu tworzących |CA| i |BC| znamy |BC|= 4 ze wzoru cosinusów wyznacz długość "l" l²= 8²+4²−2*4*8*cos120^o =................. i teraz tylko podstawić dane: P_c= πr(4+ "l " ) =........... dokończ obliczenia

Eta: Zapomniałam dorysować oś obrotu (to prosta zawierająca bok AB

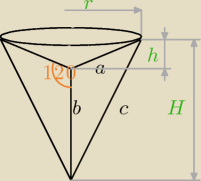
dero2005: a = 4 b = 8 c² = a²+b² − 2a*b*cos 120^o = 4² + 8² − 2*4*8*(−0,5) = 16 + 64 + 32 = 112 c = √112 = 4√7 d² = a²+a² − 2a*a*cos 120^o = 4²+4² − 2*4*4*(−0,5) = 16+16 + 16 = 48 d = √48 = 4√3

	d
r =		= 2√3
	2

h = √a² − r² = √4² − (2√3)² = √16 − 12 = √4 = 2 H = b + h = 8 + 2 = 10

	πr2
V =		(H − h) = 4π(10−2) = 32π
	3

P_c = πr(c + a) = π2√3(4√7 + 4) = 8π(√21 + √3)

Eta: I po "zabawie" ! a szkoda ..........

bryłka: Dziękuuję dla mnie to była czarna magia.