Liczby zespolone - interpretacja geometryczna.
Przypadek: |z|<2 − jak to ugryźć? Proszę o pomoc.
16 paź 22:01
ICSP: a wiesz jak wygląda |z| ?
16 paź 22:02
Przypadek: Wiem, to sprzężenie |z|=√a2+b2
16 paź 22:05
Godzio:
|z − z0| < r
Jest to środek koła (bez obwodu) o środku w z0 i promieniu r
16 paź 22:05
Godzio: Jest to koło ...
Nie wiem skąd mi tam "środek" się wziął
16 paź 22:06
Przypadek: Z0 to jaka wartość? X czy y na osi?
16 paź 22:07
Godzio:
z
0 to punkt na płaszczyźnie zespolonej, na przykład:
|z − 1 + i| < 2
Zapiszmy nieco inaczej: |z − (1 − i) | < 2
Jest to koło (bez obwodu) o środku w punkcie (1,−i) i promieniu 2
16 paź 22:08
Przypadek: Zatem moje koło ma promień 2 i środek w punkcie 0,0?
16 paź 22:09
Godzio:
16 paź 22:10
Godzio:
Tylko pamiętaj, to jest w płaszczyźnie zespolonej, a nie rzeczywistej !
16 paź 22:10
Przypadek: Dziękuję, następny przykład to |z−1|=3 czyli środek jest w punkcie 1,0?
16 paź 22:11
Godzio:
Tak
(tutaj jest już tylko OKRĄG)
16 paź 22:17
Przypadek: Ok, a następny przykład to |z−1−2i|<3, wychodzi że środek jest w punkcie (1,2i), jak
przedstawić punkt 2i na płaszczyźnie? Dziękuję bardzo za pomoc!
16 paź 22:17
Przypadek: Aha, już widzę (1,2) na płaszczyźnie, mam rację? Wielkie dzięki, bo od rana robię zadania na
studia.
16 paź 22:19
Godzio: (1,2i) na zespolonej
16 paź 22:21
Godzio:
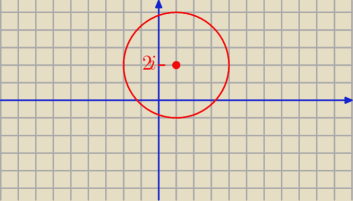
16 paź 22:22
Przypadek: Bardzo dziękuję, miałem problem głównie z wykresami ale teraz rozumiem.
16 paź 22:33