Rysowanie wykresów przekształconych funkcji,
BigMax: Zastanawia mnie to czy jest jakaś kolejność wykonywania przekształceń. Np Mam narysowaną
funkcje f(x) = 3x i mam ją tak przekształcić by zrobić z niej g(x) = | 3 |x−3| − 2 | . Od
czego zacząć rysowanie i w ogóle.
Innym przykładem może to że z funkcji f(x) = log
2x mam otrzymać g(x) = log
2(2−x). Nie
wiem jak Wy, ale ja się gubię w takich rzeczach np to zadanie z logarytmami zrobiłem najpierw
tak:
log
2[ −x + 2} więc g(x) = f(−x + 2). W książce jednak pisze, że trzeba zrobić tak g(x) =
log
2( −(x−2)) . Dlaczego tak jest. Czy są jakieś ogólne kolejności wykonywania
przekształceń? Jakieś najważniejsze zasady? Mile widziane własne przykłady

Z góry dziękuję
za pomoc
11 maj 13:04
Krzysiek: ja zaczynam od x, czyli najpierw |x−3|, potem *3, potem obniżam o dwa i całość | |.
11 maj 14:54
joanna: jak już masz funkcje 3x to proponuję rozważyć dla x>=3 czyli będzie
|3x−11| czyli najpierw obniżyć to co masz o 11 ale tylko tą część po prawej stronie x=3
a dla x<3 będzie y=−3x+7 (symetria 3x względem OX i przesunięcie o 7 w górę) i na koniec ze
wszystkiego moduł
11 maj 15:00
joanna: jak przy x jest minus to zazwyczaj od tego zaczynasz, jednak:
w tym przykładzie opisanym mógłbyś namalować logx, następnie log(−x) ale NIE MOŻESZ bo działa
tu dziedzina logarytmu x>0 a −x<0 i by się posypało
dla funkcji o dziedzinie rzeczywistej śmiało można narysować kolejno f(x), f(−x) i przesunąć o
wektor [−2,0]
11 maj 15:04
księżniczka: zawsze zaczynamy od tego co jest w środku

1 cze 14:22
asdf: wstawie kilka postów, prosze na razie nie pisać.
1 cze 14:23
asdf:
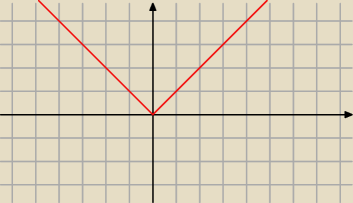
1. |x|
1 cze 14:24
asdf:
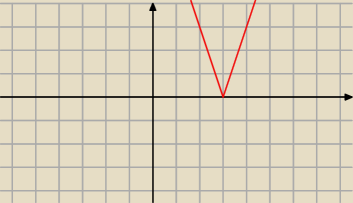
2. |x−3|
1 cze 14:25
asdf:
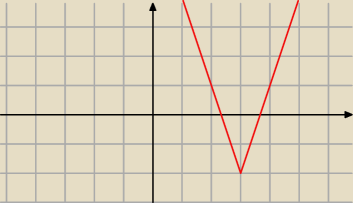
wcześniejszy post to już jest 3|x−3|
3. 3*|x−3|−2
1 cze 14:26
asdf:
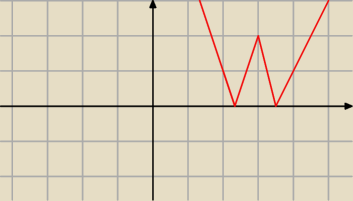
zostało odbić (ręcznie to zrobiłem, nie można tego wprowadzić w tym edytorze)
1 cze 14:29
Nina: −√−x−2+3
24 wrz 17:55
Nina: Proszę o pomoc w przykładzie powyżej
Dlaczego najpierw muszę przesunąć o 2 a potem odbić względem os OY a nie mogę na odwrót ?
24 wrz 17:57
Jerzy:
Najpierw ustal dziedzinę tej funkcji.
24 wrz 18:50
Eta:
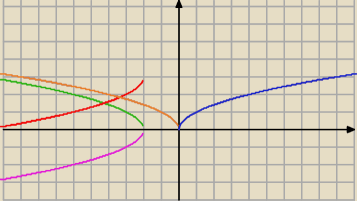
1/
y=
√x
2/ S
OY :
y=
√−x
3/ T
u[−2,0] :
y=
√−x−2
4/ S
OX :
y=−
√−x−2
5/ T
u[0,3] :
y=−
√−x−2+3
24 wrz 21:03
hj: ΩΩΩΩΩΩ
23 lut 17:57
Daris: |f(−x) +2|
5 paź 22:23
Mila:
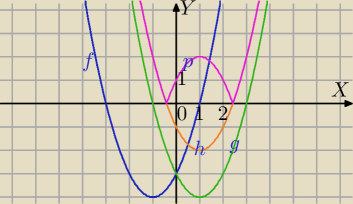
Przykład :
f(x)=x2+2x−4→Symetria względem OY ⇒
g(x)=f(−x)→T
[0,2]⇒
h(x)=f(−x)+2→Symetria S
OX tylko tej części wykresu która leży pod osią OX⇒
p(x)=|f(−x)+2|
6 paź 18:14
dsa: ∊≥
9 paź 22:14
 Z góry dziękuję
za pomoc
Z góry dziękuję
za pomoc

 1. |x|
1. |x|
 2. |x−3|
2. |x−3|
 wcześniejszy post to już jest 3|x−3|
3. 3*|x−3|−2
wcześniejszy post to już jest 3|x−3|
3. 3*|x−3|−2
 zostało odbić (ręcznie to zrobiłem, nie można tego wprowadzić w tym edytorze)
zostało odbić (ręcznie to zrobiłem, nie można tego wprowadzić w tym edytorze)
 1/ y=√x
2/ SOY : y=√−x
3/ Tu[−2,0] : y=√−x−2
4/ SOX : y=−√−x−2
5/ Tu[0,3] : y=−√−x−2+3
1/ y=√x
2/ SOY : y=√−x
3/ Tu[−2,0] : y=√−x−2
4/ SOX : y=−√−x−2
5/ Tu[0,3] : y=−√−x−2+3
 Przykład :
f(x)=x2+2x−4→Symetria względem OY ⇒ g(x)=f(−x)→T[0,2]⇒
h(x)=f(−x)+2→Symetria SOX tylko tej części wykresu która leży pod osią OX⇒
p(x)=|f(−x)+2|
Przykład :
f(x)=x2+2x−4→Symetria względem OY ⇒ g(x)=f(−x)→T[0,2]⇒
h(x)=f(−x)+2→Symetria SOX tylko tej części wykresu która leży pod osią OX⇒
p(x)=|f(−x)+2|