 1. Znaleźć miejsce geometryczne punktów równo oddalonych od punktu F(2,3) i od prostej x = −4
(zrobić rysunek ).
2. Dany wektor u = [− 3 , 4 ]. Znaleźć wektor jednostkowy (wersor) równoległy do u o zwrocie
przeciwnym do u
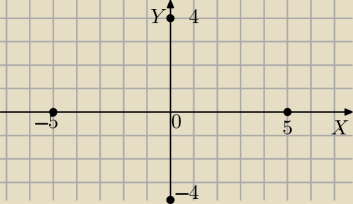
3. Znaleźć miejsce geometryczne punktów, których suma odległości od dwóch danych punktów
F1(− 3,0) i F2 ( 3,0) jest wielkością stałą równą 10 ( zrobić rysunek ).
1. Znaleźć miejsce geometryczne punktów równo oddalonych od punktu F(2,3) i od prostej x = −4
(zrobić rysunek ).
2. Dany wektor u = [− 3 , 4 ]. Znaleźć wektor jednostkowy (wersor) równoległy do u o zwrocie
przeciwnym do u
3. Znaleźć miejsce geometryczne punktów, których suma odległości od dwóch danych punktów
F1(− 3,0) i F2 ( 3,0) jest wielkością stałą równą 10 ( zrobić rysunek ).
 √(x+3)2+y2=10−√ (x−3)2+y2 /2 po podniesieniu do kwadratu i redukcji
20√x2+6x+9+y2=100−12x /2 po podniesieniu do kwadratu i redukcji
16x2+25y2=400 /:400
√(x+3)2+y2=10−√ (x−3)2+y2 /2 po podniesieniu do kwadratu i redukcji
20√x2+6x+9+y2=100−12x /2 po podniesieniu do kwadratu i redukcji
16x2+25y2=400 /:400
| 16x2 | 25y2 | ||
+ | =1⇔do postaci kanonicznej | ||
| 400 | 400 |
| x2 | y2 | ||
+ | =1 | ||
| 52 | 42 |
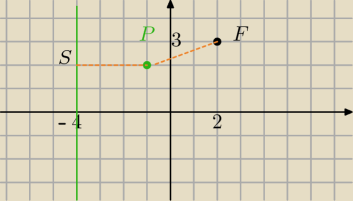 1) rysunek
P=(x,y)
S=(−4;y)
|PS|=|PF|
1) rysunek
P=(x,y)
S=(−4;y)
|PS|=|PF|
| 1 | 1 | |||
otrzymasz parabolę x= | y2− | y−3 | ||
| 12 | 2 |