Oblicz objętość graniastosłupa i pole powierzchni Zabkaka: 1) Podstawą graniastosłupa prostego jest romb. Krótsza przekątna ma długość 12 i tworzy z krawędzią podstawy kąt 60 stopni. Kąt między krótszą przekątną rombu i krótszą przekątną graniastosłupa ma miarę 30 stopni. Oblicz objętość graniastosłupa. 2) Oblicz pole powierzchni graniastosłupa prawidłowego trójkątnego w którym przekątna ściany bocznej ma długość 6 i tworzy z sąsiednią ścianą boczną kąt α. 3) Pole powierzchni bocznej graniastosłupa prawidłowego trójkątnego jest równe 108cm². Przekątna jego ściany bocznej jest dwa razy dłuższa od krawędzi podstawy. Oblicz objętość tego graniastosłupa.

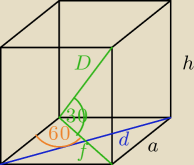
dero2005: f = 12 a = f = 12

h		√3
	= tg 30o =
f		3

h = 4√3

	√3
Pp = a2sin60o = 122*		= 72√3
	2

V = P_p*h = 864 cm³

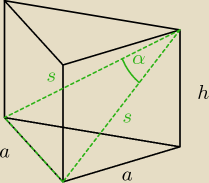
dero2005: s = 6 a² = s² + s² − 2s*s*cos α = 2s² − 2s²cos α = 2*6² − 2*6²cos α = 72(1−cosα) a = 6√2√1−cosα h = √s² − a² = 36(2cosα − 1)

	a2√2
Pc =		+ 3a*h =
	2