trygonometria prosze o pomoc malwinka: proszę o pomoc! tgα=2

	π
oblicz wartość wyrażenia1−2cos2(		−α)+2sin4(π−α)
	2

1−2sin²α+2sin⁴α

malwinka: proszE!

malwinka: wyszło mi 0,68

257: 2sin⁴α − 2sin²α + 1 = 0, 3, 5... bo jak mam niby to zrobić ?

malwinka: wiemy że tgα=2

257: Czyli wiedząc, że tgα = 2 obliczyć wartość wyrażeń?

asdf: tgx = 2 ⇒ sinx = 2cosx

257: Zatem trzeba wpierw obliczyć wartości pozostałych funkcji trygonometrycznych.

sinα
	= 2 ⇒ sinα = 2cosα
cosα

Teraz podstawiasz to do jedynki sin²α + cos²α = 1 4cos²α + cos²α = 1 5cos²α = 1

	1
cos2α =
	5

	√5		√5
cosα =		v cosα = −
	5		5

257: Teraz masz 2 przypadki: Dla każdego cosinusa wyjdzie inny sinus. Tyle...

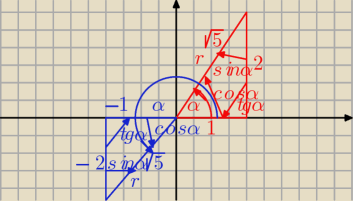
Gustlik: r²=2²+1²=5 ⇒ r=√5 Trójkąt czerwony

	2		2√5		1		√5
sinα=		=		, cosα=		=
	√5		5		√5		5

Trójkąt niebieski

	−2		2√5		−1		√5
sinα=		=−		, cosα=		=−
	√5		5		√5		5

UWAGA ! Ujemne liczby przy bokach trójkąta w III ćwiartce to współrzędne, a nie długości ! Skorzystaj teraz ze wzorów redukcyjnych:

	π
cos(		−α}=sinα, sin(π−α)=sinα, podstaw sinusa i cosinusa do tych wyrażeń i obliczysz je.
	2