oblicz pole obszaru ogarniczonego Karol: Oblicz pole obszaru ograniczonego krzywą: tg²x i prosta y=1 w jaki sposób moge dowiedzieć sie, że dla tg²x

	π		π
miejsca x −		i		prosta y=1 je przecina?
	4		4

skad mam wiedzieć, ze bedzie trzeba obliczyc calke ∫ [1−tg²x], ograniczona wlasnie w tych ww miejscach?, jak do nich dojsc?

Karol: ∫tg²x= tgx−x

	π
	4

∫ [1−tg²x]= x−(tgx−x)=x−tgx+x=2x−tgx itd?

	π
−
	4

i teraz dla tego podkladam i

Karol: ?

Karol: bardzo prosze o pomoc

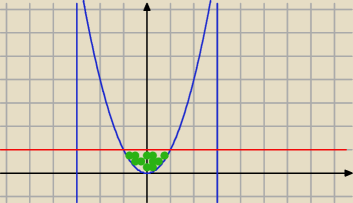
Basia: stąd i z rozwiązania równania tg²x = 1 tg²x − 1 = 0 (tgx−1)(tgx+1)=0 tgx−1=0 ∨ tgx+1=0 tgx = 1 ∨ tgx= −1

	π		π
x =		∨ x = −
	4		4

P = tak jak napisałeś albo P = 2₀∫^π/4[1−tg²x]dx

Piotr: tu masz jak w wolframie http://www.wolframalpha.com/input/?i=area+between+y%3Dtg%5E2%28x%29+%2C+y%3D1

Basia:

	sin2x
∫(1−tg2x)dx = ∫1dx − ∫tg2xdx = x − ∫		dx =
	cos2x

	1−cos2x
x − ∫		dx =
	cos2x

	1
x − [ ∫		dx − ∫1dx ] =
	cos2x

x − [tgx − x ] = 2x − tgx P = 2*[ (2*^π₄ − tg^π₄) − (2*0 − tg0) ] = 2*[ (^π₂ − 1) − (0−0) ] = 2*(^π₂ −1) = π − 2

Karol: Dzieki wielkie, ale czy aby napewno moje pole jest dobre bo niestety wychodzi wynik samo "π" przy "moim" wzorze a Ciebie wyszed "π−2" wydaje mi sie, ze nie popelnilem bledu czy aby ten zapis nie jest bledny? Czyli w podobnych tego typu zadaniach tak sie wyznacza miejsce na x, gdzie przecina dany wykres?

Karol: wyszedl*

Basia: przy Twoim zapisie to jest [2*^π₄ − tg^π₄] − [2*(−^π₄) − tg(−^π₄) ] = [^π₂ − 1] − [−^π₂ − (−1) ] = [^π₂ − 1] − [−^π₂ +1 ] = ^π₂ − 1 + ^π₂ −1 = π − 2 i nie ma inaczej oczywiście trzeba wyznaczyć punkty przecięcia, bo to będą granice całkowania