wartośc bezwzględna!! !!!!!!!!!!!!!!!!!!: rozwiąż równanie 2Ix+1I = IxI + Ix+2I

♊: Odpowiedz na pytanie: Dla jakich x podane wyrażenia są prawdziwe |x+1|=0 |x|=0 |x+2|=0 ?

!!!!!!!!!!: |x+1|=0 x=1 lub x=−1 x=0 |x+2|=0 x=2 lub x=−2

Mickej: fajnie 2+2=0

!!!!!!!!!!!!!!!!!!: x = − 1 ? x = 0 ? x = −2 ?

Damian: Mickej albo Bogdanie roztrzaskaj to zadanie bo mi |x| zawala wszystko... pliska

Mickej: ja sie nie wtrącam bo widzę że numer 2 tu rozpoczął swój proces myślowy

♊: Teraz musisz sprawdzić rozwiązania dla przedziałów ograniczonych tymi liczbami − czyli dla 1. x ∊ (−∞,−2) 2. x ∊ <−2,−1> 3. x ∊ (−1,0)> 4. x ∊ (0,+∞) (zbiory "zamykałem" w dowolnych przedziałach − chodzi tylko o to, żeby łacznie wszystkie zbiory dały zbiór liczb Rzeczywistych). We wszystkich 4 przypadkach metody postępowania są takie same: Postawiasz do równania jakąś wartość za x, następnie sprawdzasz czy wyrażenie pow wartością bezwzględną będzie dodatnie czy ujemne. biorę jakąs liczbę ze zbioru pierwszego, np −100 2I−100+1I = I−100I + I−100+2I teraz trzeba policzyć to co jest w wartości bezwzględnej 2I−99I = I−100I + I−98I Wszystkie są ujemne, więc przepisuję równanie, już bez wartości bezwzględnej, ale zmieniam znak. 2(−x−1) = −x −x−2 Jeżeli by wyszła wartość dodatnia, to by się nie zmieniało znaku, po prostu by się wyrzucało znak wartości bezwzględnej. W przypadku 2 i 3. będzie tzreba w niektórych zmienić znak, a w niektórych zostawić taki sam jak jest. Potem masz do rozwiązania zwykłe równania. Jeżeli odpowiedź wyjdzie w którymś z przypadku z poza przedziału, to nie uwzględniasz jej w odpowiedzi końcowej. Odpowiedź końcową stanowi suma rozwiązan wszystkich 4 równań.

Damian: juz wiem po prostu chodziło o to ze |x| zmienia znak w 0 i tego a ja kiedyśsię męczyłem z takimi rownaniami (wstyd mi) rozwiązywałem wart bezwzględne na przedziałach ale zawsze przy x cos stało a jak nie stało to głupiałem... dzieki

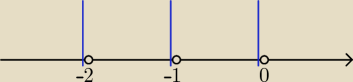
Bogdan: 2|x + 1| = |x| + |x + 2| x=−1 x=0 x=−2 Rozpatrujemy równanie w 4 przedziałach: 1. x ∊ (−∞, −2): −2(x + 1) = −x − (x + 2) −2x − 2 = −x − x − 2 0 = 0 odp.: x ∊ (−∞, −2) 2. x ∊ <−2, −1): −2(x + 1) = −x + (x + 2) −2x − 2 = −x + x + 2 −2x = 4 ⇒ x = −2 odp.: x = −2 3. x ∊ <−1, 0): 2(x + 1) = −x + (x + 2) 2x + 2 = −x + x + 2 2x = 0 ⇒ x = 0 sprzeczność, bo 0 nie należy do <−1, 0) 4. x ∊ <0, +∞): 2(x + 1) = x + (x + 2) 2x + 2 = x + x + 2 0 = 0 odp.: x ∊ <0, +∞) Odp.: x ∊ (−∞, −2> U <0, +∞)

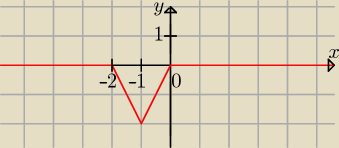
Bogdan: 2|x + 1| = |x| + |x + 2| ⇒ 2|x + 1| − |x| − |x + 2| = 0 Rozwiązaniem równania jest zbiór miejsc zerowych funkcji: f(x) = 2|x + 1| − |x| − |x + 2|, jej wykres przedstawiam na rysunku czerwonym kolorem.

♊: Bogdanie − a Ty sę przypadkiem nie pomyliłeś z tą końcową odpowiedzią ? Odpowiedzią na pytanie o x nie może być ten zbiór y dla x ∊ (−2,0) . . .

Bogdan: Nie podałem zbioru dla y, podałem jako rozwiązanie równania: x ∊ (−∞, −2> U <0, +∞). Ilustracją tego rozwiązania jest zbiór miejsc zerowych (czyli zbiór x) funkcji: f(x) = 2|x + 1| − |x| − |x + 2|

Bogdan: Przedstawiłem jak sądzę prostą i czytelną metodę rozwiązywania równań, a także nierówności ze zmiennymi w wyrażeniach bezwzględnych.

Bogdan: II − wyjaśnij swoją wątpliwość dotyczącą rozwiązania.

♊: Jeżeli masz jedna zmienną, to odpowiedzi powinny nelażeć do zbioru liczb rzeczywistych a nie, jak to u Ciebie wygląda, do iloczynu kartezjańskiego.

♊: A! źle zrozumiałem Twoją wcześniejszą wypowiedź. Odczytałęm ją tak: Rozwiązaniem równania jest zbiór miejsc zerowych funkcji: f(x) = 2|x + 1| − |x| − |x + 2|, jej wykres przedstawiam na rysunku czerwonym kolorem. Wybacz − mój błąd . . .

Bogdan: Jeszcze raz podkreślam, rozwiązaniem równania jest x ∊ (−∞, −2> U <0, +∞). Gdzie tu masz iloczyn kartezjański? Rysunek, który załączyłem, jest tylko ilustracją, a nie rozwiązaniem.

♊: A bo ja mam problemy z koncentracją o tej porze już Przed chwilą nie mogłem poprawnie napisać funkcji sortującej tablicę, teraz nie zwracam uwagi na 3/4 czyjejś wypowiedzi . . . Chyba czas iść spać ;P