!!!!!! POMOCY :o: 1. Prostokąt ABCD jest podstawą ostrosłupa ABCDS. Dwie jego sąsiednie ściany boczne są prostopadłe do płaszczyzny podstawy. Oblicz objętość ostrosłupa, wiedząc, że dwie pozostałe ściany boczne są nachylone do płaszczyzny podstawy pod kątami 30 i 60 stopni, a wysokość ostrosłupa jest równa √3. *Jak będzie wyglądać siatka tego ostrosłupa? Proszę o pełne rozwiązanie zadania

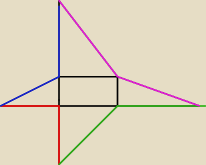
aniab: siatka odcinki o tych samych kolorach są równe czerwony to wysokość i wynosi √3

aniab: w dolnym trójkącie kąt między zielonym a czarnym = 30° w bocznym trójkącie kąt między niebieskim a czarnym 60° trójkaty prostokątne .. bok i kąty znasz .. mozesz obliczyc boki prostokąta

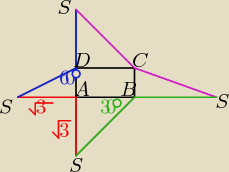
aniab: AB = 3 AD=1 V=1/3 * 1*3*√3 = √3

aa: podstawą ostrosłupa ABCDS jest kwadrat ABCD. Ściana boczna ADS jest trójkątem równobocznym o polu 81√3 leżącym w płaszczyźnie prostopadłej do płaszczyzny podstawy a. oblicz objętość tego ostrosłupa b. oblicz sumę długości wszystkich krawędzi tego ostrosłupa

Aga1.:

	a2√3
Ze wzoru na pole trójkąta równobocznego P=		=81√3
	4

z tego oblicz a ( długość 6 krawędzi) Ze wzoru na wysokość w trójkącie równobocznym oblicz wysokość ostrosłupa.

	a√3
h=		=
	2

	1
V=		a2*h=
	3

b)Suma krawędzi =6a+2b Jak policzyć b (długość krawędzi)?