rozw. nierownosc wwe: |x+1| − |x| >0

ZKS: |x + 1| > |x| x + 1 > x ∨ x + 1 < −x

wwe: czy mozna to rozwiazac takim sposobem ? https://matematykaszkolna.pl/strona/1805.html

ZKS: Jasne Twój cyrk Twoje małpki.

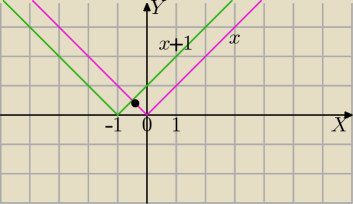
Mila: Metoda graficzna. |x+1| − |x| >0⇔|x + 1| > |x| f(x)=|x+1| (zielony wykres) g(x)=|x| (różowy wykres) znajduję punkt przecięcia x−=x+1

	1
x=−
	2

F(x) >g(x) Należy odpowiedzieć dla jakich x wykres f(x) leży powyżej wykresu g(x)

	1
dla x>−
	2

pigor: ... lub np. |x+1|−|x| >0 ⇔ |x+1| >|x| /² ⇔ (x+1)² >x² ⇔ ⇔ x²+2x+1 >x² ⇔ 2x+1 >0 ⇔ x>−¹₂ . ...

wwe: a skad to rownanie x−=x+1 ?

pigor: hmm ... zastanawiam się ZKS co tam u ciebie powyżej jednak nie gra w tej alternatywie (dobra ale dla równania) a nie chce mi się rozpisywać tak "po bożemu" ....

Mila: Algebraicznie: |x+1| − |x| >0 Rozważam przedziały. x+1≥0⇔x≥−1 x≥0 1) x<−1 obydwa wyrażenia ujemne −x−1−(−x)>0 −1>0 brak rozwiązań 2) x∊<−1;0) x+1−(−x)>0 2x+1>0

	−1
x>		i x<0
	2

=========== 3) x≥0 x+1−x>0⇔1>0 dla każdego x≥0 ========

	−1
odp x>
	2

ZKS: pigor bo źle zrobiłem powinno być: |x| < |x + 1| x < x + 1 ∨ x > −x − 1

wwe: Mila czy moglabys mi rozpisac bardziej metode algebraiczna cos mi swita ale mniej niz wiecej . Z gorydziekuje za pomoc

pigor: ... no właśnie, tak, ale wtedy musisz dać koniunkcję ∧ , wtedy będzie o. k. . ...

ZKS: Oczywiście że ∧ dzięki za poprawkę już się zagalopowałem.

Mila: Mogę napisać objaśnienia; do 1) dla x<−1 |x+1|=−x−1 |x|=−x 2) |x+1|=x+1 bo jest nieujemne dla x∊<−1;0) |x|=−x bo jest ujemne 3) dla x≥0 obydwa wyrażenia dodatnie to |x+1|=x+1 |x|=x Czy, to Ci wyjaśnia problem?

wwe: wybacz czarna magia dla mnie ... . spróbujmy tym sposobem (jest dosc zrozumialy ) https://matematykaszkolna.pl/strona/1805.html |x+1|−|x|>0 *wyznaczam miejsca zerowe czyli x=−1 i x=0 rozw nierownosc w trzech przedzialach (−niesk; −1> , (−1;0) , <0; niesk) ale srodkowy przedzial wychodzi zbior pusty jak to zapisac co z tego bd ?

wwe: z pierwszego przedzialu wychodzi mi x<−1

Mila: wwe przecież tak zrobiłam, jak w linku. Jeszcze raz . x<−1 to |x+1|=−x−1 i |x|=−x obydwa wyrażenia są ujemne, to zmieniamy znak na przeciwny. ( czy rozumiesz , że |−3|=3? |−7|=7|) to nierówność tak wygląda: −x−1−(−x)>0⇔−x−1+x>0 ⇔−1>0 sprzeczność− brak rozwiązań w tym przedziale. Przeanalizuj.

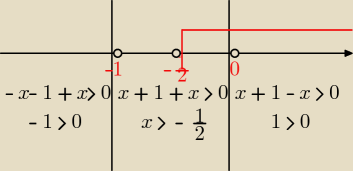
Bogdan: Można i tak:

	1
Odp.: x ∊ (−		, +∞)
	2

Basia: najładniej i najprościej to rozwiązał pigor tylko uwaga: nie zawsze tak się da

Gustlik: Basiu, też to chciałem napisać, jeżeli byłoby np. tak: |x+1| − |x| >2, to metodą pigora nie da rady. Ja proponuję zapoznac się z metodą "osi i tabelki" do tego typu zadań − jest przejszysta i nieskomplikowana, jest podobna do metody Bogdana: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=1796 . Tylko że w przypadku nierówności rozwiązaniem każdego przypadku będzie część wspólna wyniku danej nierówności i odpowiedniego założenia, a rozwiązaniem całkowitym − suma przedziałów będących rozwiązaniami poszczególnych przypadków. Czyli: 1^o) N₁∩Z₁ 2^o) N₂∩Z₂ 3^o) N₃∩Z₃ itd... gdzie N − wynik nierówności, Z − założenie. całość: 1^o)U2^o)U3^o)U... itd. wszystkie przypadki.

pigor: ...a jak ma się w tym przypadku "to cudo " do czasu na maturze , a czy da , ... czy nie da ... to da radę i tu |x+1}−|x| >2 "moja, ale i nie moja" metoda, tylko po co , ale na pewno nie jest tu i teraz ta jedyna najlepsza z tabelką − jak każda zresztą − przereklamowana , bowiem tu, dla mnie najlepsza, ale nie reklamowana, choć zasługuje na to często, ale i nie na zawsze, jest właśnie graficzna , która daje "od ręki" rozwiązanie x∊∅, co widać bez żadnych wątpliwości, bo nieprawda, że |x+1| >|x|+2 ... no i tyle . ... −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

Mila: Najważniejsze− wybór metody w zależności od typu równania. Nie ma jedynie słusznej metody. Zgadzam się z Pigorem.